Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB=BC.cos60^0=a\) ; \(AC=BC.sin60^0=a\sqrt{3}\)
\(AH=\frac{AB.AC}{BC}=\frac{a\sqrt{3}}{2}\)
a/ Do \(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC) \(\Rightarrow\widehat{SAH}=60^0\)
\(\Rightarrow SH=AH.tan60^0=\frac{3a}{2}\)
b/ \(AC^2=HC.BC\Rightarrow HC=\frac{AB^2}{BC}=\frac{3a}{2}\)
\(EH||AB\Rightarrow\frac{EH}{AB}=\frac{HC}{BC}\Rightarrow EH=\frac{AB.HC}{BC}=\frac{3a}{4}\)
Do \(SH\perp\left(ABC\right)\Rightarrow\widehat{SEH}\) là góc giữa SE và (ABC)
\(tan\widehat{SEH}=\frac{SH}{EH}=2\)
c/ Không biết (SH3) là gì bạn?

S A B C D O H
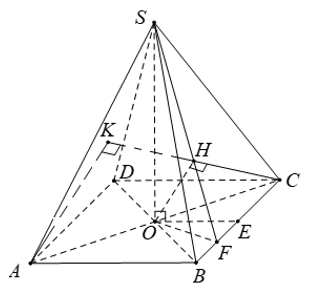
Do \(\left\{{}\begin{matrix}SA=SC\\SB=SD\end{matrix}\right.\) \(\Rightarrow\) hình chiếu vuông góc của S lên đáy trùng tâm đáy
\(\widehat{BAD}=60^0\Rightarrow\Delta BAD\) đều \(\Rightarrow BD=a\Rightarrow OB=\frac{a}{2}\)
\(\Rightarrow SO=\sqrt{SB^2-OB^2}=\frac{a\sqrt{11}}{2}\)
b/ Kẻ \(OH\perp AB\Rightarrow AB\perp\left(SOH\right)\Rightarrow\widehat{SHO}\) là góc giữa (SAB) và (ABCD)
\(OH=\frac{1}{2}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\Rightarrow tan\varphi=\frac{SO}{OH}=\frac{2\sqrt{33}}{3}\)

a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:




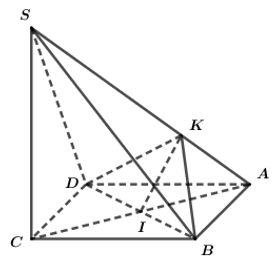





a: \(SA=\sqrt{\left(\dfrac{a}{2}\right)^2\cdot2}=\sqrt{2}\cdot\dfrac{a}{\sqrt{2}}=a\)
\(SB=SA=a\)
AH=a/2; AD=a; góc A=120 độ
=>\(cosA=\dfrac{\dfrac{1}{4}a^2+a^2-DH^2}{2\cdot\dfrac{1}{2}a\cdot a}\)
=>\(\dfrac{5}{4}a^2-HD^2=a^2\cdot\dfrac{-1}{2}=\dfrac{-1}{2}a^2\)
=>HD^2=7/4a^2
=>\(HD=\dfrac{a\sqrt{7}}{2}\)
\(SD=\sqrt{SH^2+HD^2}=\sqrt{\dfrac{7}{4}a^2+\dfrac{1}{4}a^2}=a\sqrt{2}\)
Vì SA^2+AD^2=SD^2 và AS=AD
nên ΔASD vuôg cân tại A
(SD;BC)=(DS;DA)=góc SDA=45 độ