Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Cách giải:
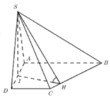
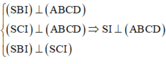
Kẻ IH
⊥
CD ta có: 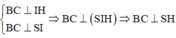
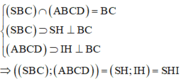
Ta có: 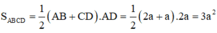
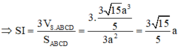
Gọi E là trung điểm của AB => EC = AD = 2a
![]()
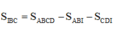
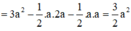
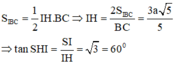


Đáp ván A
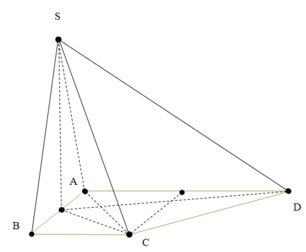
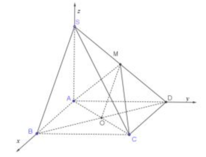
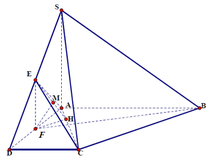
Vì I là hình chiếu của S trên (ABCD)
⇒ ( S C → , ( A B C D ) ) = S C I ⏞
⇒ S I = I C . tan 60 ° = a 5 2 . tan 60 ° = a 15 2
Vậy
V S . I B C = V S . A B C D - V S . A I B - V S . I C D = 1 3 . a 15 2 a + 2 a 2 . a - 1 2 . a 2 . 2 a - 1 2 . a 2 . a = a 3 15 8

Đáp án B
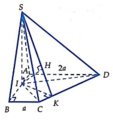
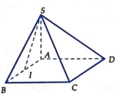
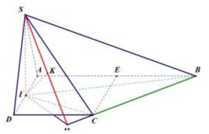
S I C D = S A B C D − S A I D − S B I C = 3 a 2 − a 2 − a 2 2 = 3 a 2 2 ; C D = 2 a 2 + a 2 = a 5
Gọi K, H lần lượt là hình chiếu của I lên CD và SK
⇒ I H ⊥ S C D ⇒ I H = d I ; S C D = 3 a 2 4
S Δ I C D = 1 2 I K . C D ⇒ I K = 2 S I C D C D = 3 a 2 a 5 = 3 a 5
1 I H 2 = 1 I K 2 + 1 I S 2 ⇒ 1 I S 2 = 8 9 a 2 − 5 9 a 2 = 1 3 a 2 ⇒ I S = a 3
⇒ V S . A B C D = 1 3 .3 a 2 . a 3 = a 3 3

Đáp án là D
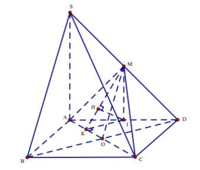
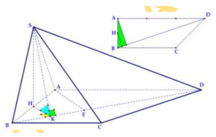
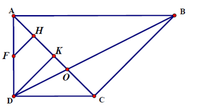
+ Gọi O là giao điểm của AC,BD
⇒ MO \\ SB ⇒ SB \\ ACM
⇒ d SB,ACM = d B,ACM = d D,ACM .
+ Gọi I là trung điểm của AD ,
M I \ \ S A ⇒ M I ⊥ A B C D d D , A C M = 2 d I , A C M .
+ Trong ABCD: IK ⊥ AC (với K ∈ AC ).
+ Trong MIK: IH ⊥ MK (với H ∈ MK ) (1) .
+ Ta có: AC ⊥ MI ,AC ⊥ IK ⇒ AC ⊥ MIK
⇒ AC ⊥ IH (2) .
Từ 1 và 2 suy ra
IH ⊥ ACM ⇒ d I ,ACM = IH .
+ Tính IH ?
- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .
- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4
⇒ I H = a a 2 4 a 2 + a 2 8 = a 3
Vậy d S B , A C M = 2 a 3 .
Lời giải khác


Đáp án D
Ta có: f ' x = x − 1 x 2 − 2 2 x 2 + 2 đổi dấu khi đi qua điểm x=1 nên hàm số đã cho có duy nhất 1 điểm cực trị.
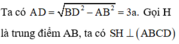
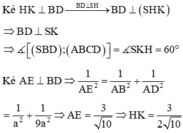




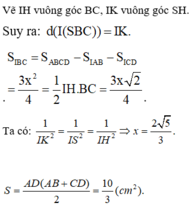
Đáp án D.
Ta có
B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ ( S A B ) ⇒ B C ⊥ S I
Gọi H là hình chiếu của B lên SI ⇒ B H ⊥ S I B H ⊥ B C ⇒ B H = d ( B C ; S I )
⇒ Δ B H I ∽ Δ S A I ⇒ B H S A = B I S I ⇒ B H = S A . B I S I = a 3 . a 2 a = a 3 2