Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
- Sử dụng phương pháp tọa độ trong không gian, gắn hệ trục tọa độ gốc A và các trục tọa độ sao cho

- Sử dụng các công thức điểm, véc tơ, mặt phẳng, góc giữa hai mặt phẳng để tính toán.
Cách giải:
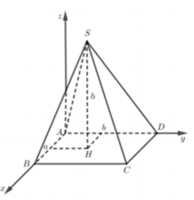
Gắn hệ trục tọa độ như hình vẽ, giả sử ABCD là hình vuông cạnh l,
chiều cao hình chóp SH = h.
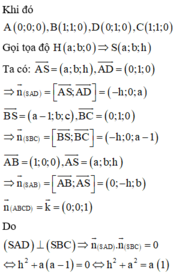
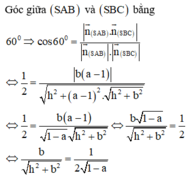
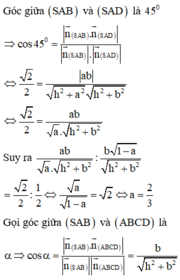
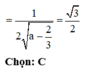

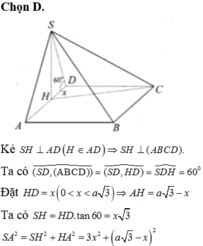
Đáp án B
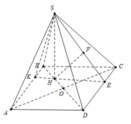
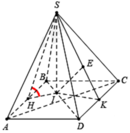
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14

Đáp án A
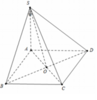
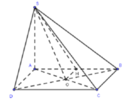
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .

Chọn đáp án C
Ta có
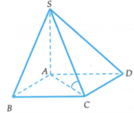
⇒ A C là hình chiếu của SC trên mặt phẳng (ABCD)
![]()
Lại có ABCD là hình vuông cạnh a nên A C = a 2
Tam giác SAC vuông tại A nên S A = A C . tan S C A ⏜ = a 6
Vậy thể tích khối chóp S.ABCD là V A B C D = a 3 6 3 (đvtt).

Đáp án D
Phương pháp:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
Gọi H là trung điểm của AB => OH//AD
ABCD là hình vuông => AD ⊥ AB; OH ⊥ AB
Mà OH ⊥ SA, (vì SA ⊥ (ABCD))
=> OH ⊥ (SAB)
=>SH là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
=> (SO,(SAB)) = (SO,SH) = HSO
Ta có: OH là đường trung bình của tam giác ABD 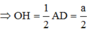
Tam giác SAH vuông tại A ![]()
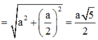
Tam giác SHO vuông tại H: 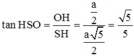

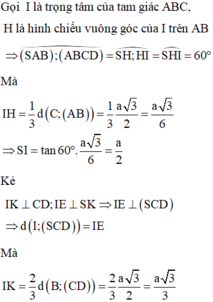
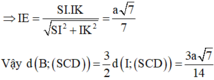



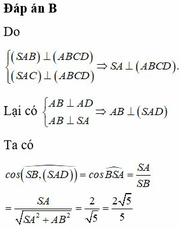
Đáp án là D