Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BH vuông góc SA
BH vuông góc AC
=>BH vuông góc (SAC)
b: (SC;ABCD)=(CS;CA)=góc SCA
\(AC=\sqrt{a^2+\left(\dfrac{1}{5}a\right)^2}=\dfrac{a\sqrt{26}}{5}\)
\(SC=\sqrt{SA^2+AC^2}=\dfrac{3\sqrt{14}}{5}\)a
\(sinSCA=\dfrac{SA}{SC}=\dfrac{2a}{\dfrac{3\sqrt{14}}{5}a}=\dfrac{5\sqrt{14}}{21}\)
=>góc SCA=63 độ

Lời giải:
$SA\perp AB$, $SA\perp AD$ mà $AB, AD$ cùng nằm trên mặt phẳng $(ABCD)$ nên $SA\perp (ABCD)$.
Mà \(BD\subset (ABCD)\) nên $SA\perp BD$ (đpcm)

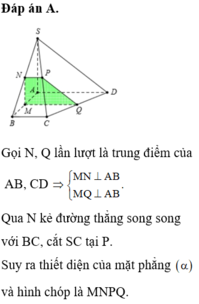
Đáp án C
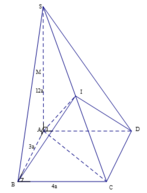
Gọi I là trung điểm SC
Tam giác SAC vuông tại A, ta có: IA = IS = IC
=> ∆ SBC vuông tại B, ta có IB = IS = IC
Tương tự ta có ID = IS = IC
Vậy I là tâm mặt cầu ngoại tiếp hình chóp và bán kính bằng 1 2 SC
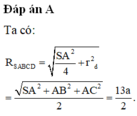
Tam giác ABC vuông tại B, ta có: AC = ![]()
Tam giác SAC vuông tại A, ta có SC = ![]()
Vậy bán kính đường tròn ngoại tiếp hình chóp là: R = 13 a 2
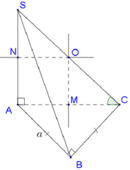



Ta có: SA\(\perp\)AB
SA\(\perp\)AC
AB,AC cùng thuộc mp(ABC)
Do đó: SA\(\perp\)(ABC)
=>SA\(\perp\)BC
=>\(\widehat{\left(SA;BC\right)}=90^0\)