Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
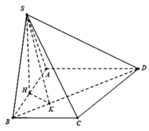
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: 
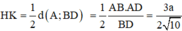
Do đó 
Vậy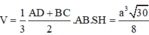 
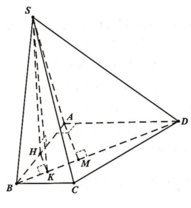
Vẽ S H ⊥ A C tại H.
Khi đó: ( S A C ) ⊥ ( A B C D ) ( S A C ) ⊥ ( A B C D ) = A C S H ⊂ ( S A C ) S H ⊥ A C
⇒ S H ⊥ ( A B C D ) ⇒ V = 1 3 S H . S A B C D
Theo đề ∆ S A C vuông tại S nên ta có:
S C = A C 2 - S A 2 = 6 a 2
và S H = S A . S C A C
= 2 a 2 . 6 a 2 2 a = 6 a 4
Vậy V = 1 3 S H . S A B C D = 6 a 3 12
Chọn đáp án A.
Đáp án B
Diện tích hình thang ABCD là:
S A B C D = A B . A D + B C 2 = 5
Vậy thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . S A . S A B C D = 1 3 .2.5 = 10 3 (đvtt)
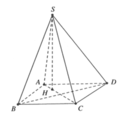
Ta có S C D ∩ A B C D = C D
C D ⊥ S A C D ⊥ A C ⇒ C D ⊥ S A C ⇒ S C ⊥ C D
Vì S C ⊥ C D , S C ⊂ S C D A C ⊥ C D , A C ⊂ A B C D
Nên S C D , A B C D ^ = S C A ^ = 45 o
Dễ thấy ∆ S A C vuông cân tại A
Suy ra SA = AC = a 2
Lại có
S M C D = 1 2 M C . M D = 1 2 a . a = a 2 2
Do đó
V = V S . M C D = 1 3 S M C D S A = 1 3 . a 2 2 . a 2 = a 3 2 6
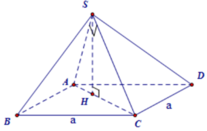
Ta có
B D ∥ M N M N ⊂ S M N ⇒ B D ∥ S M N
Khi đó d( SM,BD ) = d( SM, (SMN) ) = d( D, (SMN) ) = d( A, ( SMN) )
Kẻ A P ⊥ M N , P ∈ M N A H ⊥ S P , H ∈ S P
Suy ra A H ⊥ S M N ⇒ d A S M N = A H
∆ S A P vuông tại A có
1 A H 2 = 1 S A 2 + 1 A P 2 = 1 S A 2 + 1 A N 2 + 1 A M 2 = 1 2 a 2 + 1 a 2 4 + 1 a 2 = 11 2 a 2
Do đó d = d( SM, BD ) = AH = a 22 11
Đáp án A
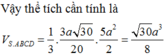
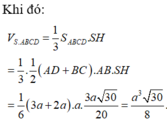
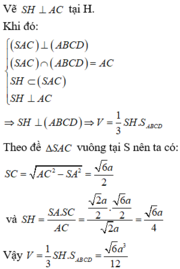
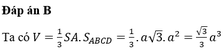
Chọn D.