Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

a: (SB;(ABCD))=(BS;BA)=góc SBA
AC=căn a^2+3a^2=2a
SA=căn SC^2-AC^2=a*căn 3
tan SBA=SA/AB=căn 3
=>góc SBA=60 độ
b: (SC;(SAD))=(SC;SD)=góc SCD
SD=căn SA^2+AD^2=2a*căn 3
cos SCD=(CS^2+CD^2-SD^2)/(2*CS*CD)=-2/căn 7
=>góc SCD=139 độ

a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ

a: SA\(\perp\)(ABC)
=>SA\(\perp\)AB; SA\(\perp\)AC; SA\(\perp\)BC
=>ΔSAB vuông tại A và ΔSAC vuông tại A
Ta có: ΔABC vuông cân tại B
=>BA=BC=a và \(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\widehat{SA;AB}=\widehat{SAB}=90^0\)
b: \(\widehat{SB;BA}=\widehat{SBA}\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{2}}{a}=\sqrt{2}\)
nên \(\widehat{SBA}\simeq54^044'\)
=>\(\widehat{SB;BA}\simeq54^044'\)

a.
Do tam giác SAB đều \(\Rightarrow SB=AB=a\)
Trong tam giác SBC ta có:
\(SB^2+BC^2=2a^2=SC^2\)
\(\Rightarrow\Delta SBC\) vuông tại B (pitago đảo)
\(\Rightarrow BC\perp SB\)
Mà \(BC\perp AB\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
Do \(SH\in\left(SAB\right)\Rightarrow BC\perp SH\) (1)
Lại có SAB là tam giác đều, mà SH là đường trung tuyến (H là trung điểm AB)
\(\Rightarrow SH\) đồng thời là đường cao hay \(SH\perp AB\) (2)
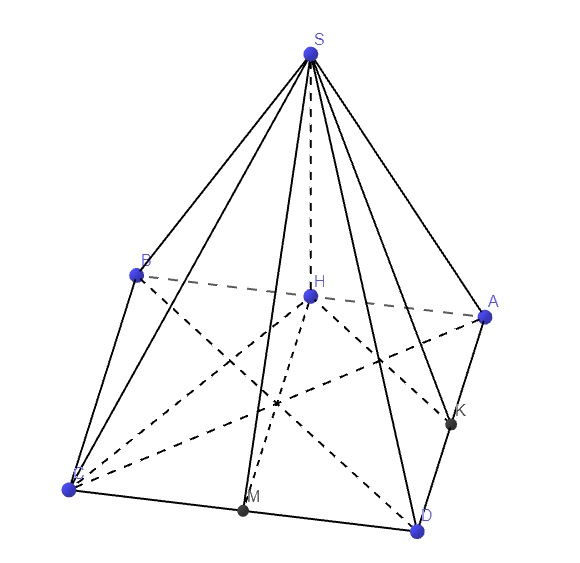
(1);(2) \(\Rightarrow SH\perp\left(ABCD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) HM là hình chiếu vuông góc của SM lên (ABCD)
\(\Rightarrow\widehat{SMH}\) là góc giữa SM và (ABCD) hay \(\alpha=\widehat{SMH}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(HM=BC=a\) \(\Rightarrow tan\alpha=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
c.
Do H là trung điểm AB, K là trung điểm AD \(\Rightarrow\) HK là đường trung bình tam giác ABD
\(\Rightarrow HK||BD\)
Mà \(BD\perp AC\) (hai đường chéo hình vuông)
\(\Rightarrow HK\perp AC\) (3)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\) (4)
(3);(4) \(\Rightarrow AC\perp\left(SHK\right)\Rightarrow AC\perp SK\)

Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)


a: (SB;(ABC))=(BS;BA)=góc SBA
BA^2+BC^2=AC^2
=>2*BA^2=AC^2
=>AB=BC=a
tan SBA=SA/SB=căn 3
=>góc SBA=60 độ
d: (SB;(BAC))=(BS;BA)=góc SBA=60 độ
e:
CB vuông góc AB
CB vuông góc SA
=>CB vuông góc (SBA)
=>(SC;(SBA))=(SC;SB)=góc BSC
SB=căn SA^2+AB^2=2a
SC=căn SA^2+AC^2=a*căn 5
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
sin BSC=BC/SC=a/a*căn 5=1/căn 5
=>góc BSC\(\simeq27^0\)