Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S B H C I A D
Gọi I là trung điểm của AD.
Ta có : \(IA=ID=IC=a\Rightarrow CD\perp AC\)
Mặt khác, \(CD\perp SA\) suy ra CD vuông góc với SC nên tam giác SCD là tam giác vuông tại C
Trong tam giác vuông SAB ta có :
\(\frac{SH}{SB}=\frac{SA^2}{SB^2}=\frac{SA^2}{SA^2+AB^2}=\frac{2a^2}{2a^2+a^2}=\frac{2}{3}\)
Gọi \(d_{1,};d_2\) lần lượt là khoảng cách từ B và H đến mặt phẳng (SCD) thì
\(\frac{d_2}{d_1}=\frac{SH}{SB}=\frac{2}{3}\Rightarrow d_2=\frac{2}{3}d_1\)
\(d_1=\frac{3V_{B.SCD}}{S_{SCD}}=\frac{SA.S_{BCD}}{S_{SCD}}\)
\(S_{NCD}=\frac{1}{2}AB.BC=\frac{1}{2}a^2\)
\(S_{SCD}=\frac{1}{2}SC.CD=\frac{1}{2}\sqrt{SA^2+AB^2+BC^2}.\sqrt{IC^2+ID^2}=a^2\sqrt{2}\)
Suy ra \(d_1=\frac{a}{2}\)
Vậy khoảng cách từ H đến mặt phẳng (SCD) là \(d_2=\frac{2}{3}d_1=\frac{a}{3}\)

a) Dễ dàng chứng minh tam giác ABC và ACD đều
Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)
\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)
b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ
Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az
Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)
\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)
theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1
\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)
Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD
\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)
\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)
Bạn ơi bạn chỉ mình cách bình thường được ko? Vì mình chưa học tọa độ hóa.

Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà

Đáp án B
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
Ta có
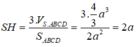
Ta lại có


S o B H A D G d H' C K
Câu a bạn tự tính nhé!
Câu b: Qua G kẻ đường thẳng d // CD , khoảng cách từ \(d\left(G;\left(SAB\right)\right)=d\left(d;\left(SAD\right)\right)\)
Kẻ HH' vuông CD , nối SH'. Lúc này SH' cách d tại K . \(d\left(K;\left(SAB\right)\right)\) là khoảng cách cần tìm.
Ta có: SH'AB =\(\frac{1}{2}S_{ABCD}\)=\(\frac{1}{2}\times2\sqrt{3}a^2=\sqrt{3}a^2\) \(\Rightarrow HH'=\frac{\sqrt{3}a^2}{a}=\sqrt{3}a\)
Vì K nằm trên d nên \(d\left(K;\left(SAB\right)\right)=\frac{2}{3}HH'=\frac{2\sqrt{3}a}{3}\)

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
2) Ta có tam giác SAB đều nên SA =a3√2
suy ra V=13SABCD.SH=a33√6

A B C D S E K H
Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)
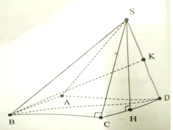


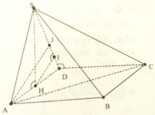


Đáp án C
Gọi H là trung điểm của CD, dễ thấy SH là đường cao của hình chóp.
Suy ra
Để ý rằng SB 2 = SH 2 + BH 2 = SH 2 + BC 2 + CH 2 = 3 a 2 / 4 + a 2 + a 2 / 4 = 2 a 2 .
Suy ra BS = BD = a 2 , gọi K là trung điểm của SD ta có: