
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



S M H G N A O D C
Ta có \(\begin{cases}BC\perp SA\\BC\perp AB\end{cases}\)\(\Rightarrow BC\perp\left(SAB\right)\)\(\Rightarrow BC\perp AM\) (vì \(AM\subset\left(SAB\right)\left(1\right)\)
Mặt khác \(SC\perp\alpha\Rightarrow SA\perp AM\) (vì \(AM\subset\alpha\)) (2)
Từ (1) và (2) suy ra \(AM\perp\left(SBC\right)\Rightarrow AM\perp MG\) (vì \(MG\subset\left(SBC\right)\))
\(\Rightarrow\Delta AMG\) vuông tại M, tương tự ta cũng có tam giác ANG vuông tại N \(\Rightarrow\) tâm H đường tròn đáy của (H) là trung điểm AG, có bán kính \(R=\frac{AG}{2}\)
Xét tam giác vuông SAC tại A có \(AG=\frac{SA.AC}{SC}=\frac{\sqrt{6}}{3}a\Rightarrow R=\frac{\sqrt{6}}{6}a\)
Vì OH là đường cao (H)\(\Rightarrow OH\perp\alpha\Rightarrow OH\)//\(SC\Rightarrow O\) là giao điểm hai đường chéo AC, BD
\(\Rightarrow OH=\frac{1}{2}CG\).
Xét tam giác vuoongSAC có AG là đường cao, nên \(CG=\frac{AC^2}{SC}=\frac{2}{\sqrt{3}}a\Rightarrow OH=\frac{\sqrt{3}}{3}a\)
Vậy thể tích hình nón là \(V_{\left(H\right)}=\frac{1}{3}\pi.R^2.OH=\frac{\sqrt{3}}{54}\pi a^3\)

A B C D S M H
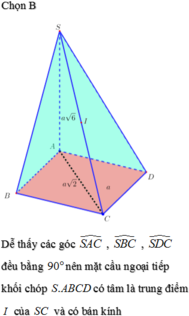
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}\Rightarrow\Delta ABC\) đều
\(\Rightarrow AM=\frac{a\sqrt{3}}{2}\Rightarrow S_{ABCD}=\frac{a^3\sqrt{3}}{2}\)
Tam giác SAM vuông tại A có \(\widehat{SMA}=45^0\Rightarrow\) Tam giác SAM vuông tại A : SA = AM = \(\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{a^3}{4}\)
Do AD song song với BC nên d(D;(SBC))=d(A,(SBC))
Gọi H là hình chiếu vuông góc của A trên SM
Ta có : \(\begin{cases}AM\perp BC\\SA\perp BC\end{cases}\)\(\Rightarrow BC\perp\cdot\left(SAM\right)\)
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AH\)
Ta có :
\(AH=\frac{AM\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\Rightarrow d\left(D,\left(SBC\right)\right)=\frac{a\sqrt{6}}{4}\)

1, Đổi chỗ 3 viên ở 3 đỉnh tam giác: viên dưới cùng lên đỉnh trên cùng, 2 viên ngoài cùng ở 2 bên đảo xuốn đáy
2, 8-6+2=4; 12-5+8=15; 13-10+15=18. x=15
3,
*) \(5^3+5=130;3^3+3=30;2^3+2=10;1^3+1=2\)
*) 2+3=8 hay 2.(2+3)-2=8
4+5=32 hay 4.(4+5)-4=32
5+8=60 hay 5.(5+8)-5=60
6+7=72 hay 6.(6+7)-6=72
7+8= 7.(7+8)-7=98

Qua O vẽ đường thẳng d vuông góc với (ABCD)
Khi đó d là trục đường tròn ngoại tiếp hình vuông ABCD
Gọi H là trung điểm của cạnh SA
Trong mặt phẳng (SAO) đường trung trực của đoạn SA cắt đường thẳng SO tại I , ta có: \(\Delta SAO\) đòng dạng \(\Delta SIH\)
\(\Rightarrow\dfrac{SA}{SO}=\dfrac{SI}{SH}\Leftrightarrow SI=\dfrac{SA.SH}{SO}=\dfrac{SA^2}{2SO}\)
Mà \(SA^2=SO^2+OA^2=\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=\dfrac{3a^2}{4}\)
\(\Leftrightarrow SA=\dfrac{a\sqrt{3}}{2}\)
Khi đó \(SI=\dfrac{3a^2}{\dfrac{4}{2.\dfrac{a}{2}}}=\dfrac{3a}{4}\)
Mặt khác \(\left\{{}\begin{matrix}IS=IA\\IA=IB=IC=ID\end{matrix}\right.\)
\(\Rightarrow IS=IA=IB=IC=ID=\dfrac{3a}{4}\)
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là I và bán kính \(R=SI=\dfrac{3a}{4}\)
Diện tích mặt cầu là: \(S=4\pi R^2=4\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{4}\)
Thể tích khối cầu là: \(V=\dfrac{4}{3}\pi R^2=\dfrac{4}{3}\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{16}\)

D A B C N M I G H
\(d\left(M,BN\right)=\frac{\left|13\left(-1\right)-10.2+13\right|}{\sqrt{13^2+10^2}}=\frac{20}{\sqrt{269}}\)
\(H\in\Delta\Leftrightarrow H\left(3a;2a\right)\)
Gọi I là tâm ABCD, G là giao điểm của AC và BN. Ta thấy G là trọng tâm của tam giác BCD
Suy ra \(CG=\frac{2}{3}.CI=\frac{1}{3}AC\) mà \(AM=\frac{1}{4}AC\Rightarrow MG=\frac{5}{12}AC\Rightarrow CG=\frac{4}{5}MG\)
\(\Rightarrow d\left(C,BN\right)=\frac{4}{5}d\left(M,BN\right)=\frac{16}{\sqrt{269}}\Rightarrow d\left(H,BN\right)=2d\left(C,BN\right)=\frac{32}{\sqrt{269}}\)
\(\Leftrightarrow\frac{\left|13.3a-10.2a+13\right|}{\sqrt{269}}=\frac{32}{\sqrt{269}}\Leftrightarrow a=1\) hoặc \(a=\frac{-45}{19}\)
Vì H và M nằm khác phía đối với đường thẳng BN nên \(H\left(3;2\right)\)
Tiếp.........
Ta thấy \(CM=\frac{3AC}{4}=\frac{2AB}{4}=\frac{2CD}{4}=\frac{CD}{2}=CD=CH\Rightarrow\Delta MHN\) vuông tại M
HM có phương trình \(y-2=0\Rightarrow MN:x+1=0\Rightarrow N\left(-1;0\right)\Rightarrow C\left(1;1\right),D\left(-3;-1\right)\)
Do \(\overrightarrow{CM}=3\overrightarrow{MA}\Rightarrow A\left(\frac{-5}{3};\frac{7}{3}\right)\Rightarrow I\left(\frac{-1}{3};\frac{5}{3}\right)\Rightarrow B\left(\frac{7}{3};\frac{13}{3}\right)\)
Vậy \(A\left(\frac{-5}{3};\frac{7}{3}\right);B\left(\frac{7}{3};\frac{13}{3}\right);C\left(1;1\right);D\left(-3.-1\right)\)