Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có: C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ ( S H M ) ⇒ ⊥ H K
Mặt khác ta có H K ⊥ S M
Suy ra H K ⊥ ( S C D )
Vậy d ( A , ( S C D ) ) = D ( H , ( S C D ) ) = H K
Xét tam giác BHC vuông tại B, ta có:
H C = B H 2 + B C 2 = a 2 ⇒ S H = H C = a 2
Xét tam giác SHM vuông tại H, ta có:
1 H K 2 = 1 S H 2 + 1 M H 2 = 1 2 a 2 + 1 a 2 = 3 2 a 2 ⇒ H K = a 6 3
Đáp án C
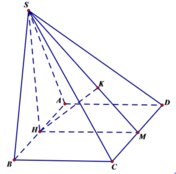
Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có: C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ ( S H M ) ⇒ ⊥ H K
Mặt khác ta có H K ⊥ ( S C D )
Suy ra H K ⊥ ( S C D )
Vậy d ( A , ( S C D ) ) = D ( H , ( S C D ) ) = H K
Xét tam giác BHC vuông tại B, ta có:
H C = B H 2 + B C 2 = a 2 ⇒ S H = H C = a 2
Xét tam giác SHM vuông tại H, ta có:
1 H K 2 = 1 S H 2 + 1 M H 2 = 1 2 a 2 + 1 a 2 = 3 2 a 2 ⇒ H K = a 6 3
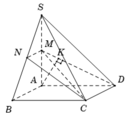
Xác định được 
Vì M là trung điểm SA nên
Kẻ 
và chứng minh được 
nên 
Trong
∆
vuông MAD tính được 
Chọn A.
Đáp án B
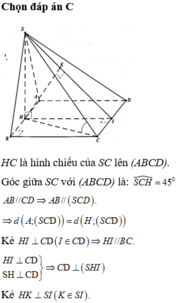
Dễ thấy: S C H ^ = 45 ∘ Gọi H là trung điểm của AB ta có S H ⊥ A B ⇒ S H ⊥ A B C D .
Ta có: S H = H C = a 17 2 .
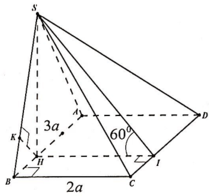
Ta có: d = d M , S A C = 1 2 d D , S A C
Mà 1 2 d D , S A C = 1 2 d B , S A C nên d = d H , S A C
Kẻ H I ⊥ A C , H K ⊥ S I ⇒ d H , S A C = H K
Ta có: H I = A B . A D 2 A C = a 5 5
Từ đó suy ra: d = H K = S H . H I S I = a 1513 89 .
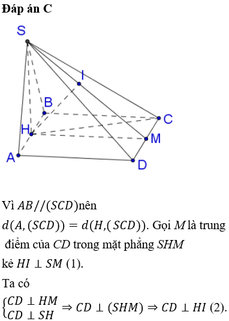
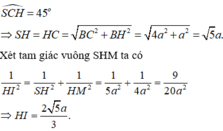
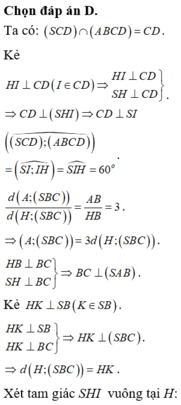
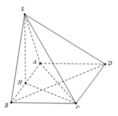
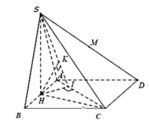
Gọi M là trung điểm CD, P là hình chiếu của H lên SM khi đó H M ⊥ C D ; C D ⊥ S H mà H P ⊥ S M ⇒ H P ⊥ S C D . Lại có A B / / C D suy ra A B / / S C D ⇒ d A ; S C D = d H ; S C D = H P
Ta có 1 H P 2 = 1 H M 2 + 1 H S 2 suy ra H P = a 6 3
Vậy d A ; S C D = a 6 3
Đáp án A