Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
Ta có: MN//AD
AD\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔDSB có
O,N lần lượt là trung điểm của DB,DS
=>ON là đường trung bình của ΔDSB
=>ON//SB và \(ON=\dfrac{SB}{2}\)
Ta có: ON//SB
ON\(\subset\)(OMN)
SB không thuộc mp(OMN)
Do đó: SB//(OMN)
c: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình của ΔASC
=>OM//SC
Ta có: OM//SC
OM\(\subset\)(OMN)
SC không nằm trong mp(OMN)
Do đó: SC//(OMN)
Ta có: SB//(OMN)
SC//(OMN)
SB,SC cùng thuộc mp(SBC)
Do đó: (SBC)//(OMN)

a.
Do M là trung điểm SA, O là trung điểm AC
\(\Rightarrow OM\) là đường trung bình tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\) (1)
N là trung điểm CD, O là trung điểm AC \(\Rightarrow ON\) là đường trung bình ACD
\(\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\) (2)
Mà \(ON\cap OM=O\) ; \(OM;ON\in\left(OMN\right)\) (3)
(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\)
b.
J cách đều AB, CD \(\Rightarrow J\) thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O \(\Rightarrow OI\) là đường trung bình tam giác SBD \(\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)\)
Hay \(IJ||\left(SAB\right)\)
- Nếu J không trùng O, ta có \(\left\{{}\begin{matrix}IO||SB\left(đtb\right)\Rightarrow IO||\left(SAB\right)\\d||AB\Rightarrow IJ||AB\Rightarrow OJ||\left(SAB\right)\end{matrix}\right.\)
\(\Rightarrow\left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)\)
a.
Do M là trung điểm SA, O là trung điểm AC
⇒��⇒OM là đường trung bình tam giác SAC ⇒��∣∣��⇒��∣∣(���)⇒OM∣∣SC⇒OM∣∣(SBC) (1)
N là trung điểm CD, O là trung điểm AC ⇒��⇒ON là đường trung bình ACD
⇒��∣∣��⇒��∣∣��⇒��∣∣(���)⇒ON∣∣AD⇒ON∣∣BC⇒ON∣∣(SBC) (2)
Mà ��∩��=�ON∩OM=O ; ��;��∈(���)OM;ON∈(OMN) (3)
(1);(2);(3) ⇒(���)∣∣(���)⇒(OMN)∣∣(SBC)
b.
J cách đều AB, CD ⇒�⇒J thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O ⇒��⇒OI là đường trung bình tam giác SBD ⇒��∣∣��⇒��∣∣(���)⇒OI∣∣SB⇒OI∣∣(SAB)
Hay ��∣∣(���)IJ∣∣(SAB)
- Nếu J không trùng O, ta có {��∣∣��(đ��)⇒��∣∣(���)�∣∣��⇒��∣∣��⇒��∣∣(���){IO∣∣SB(đtb)⇒IO∣∣(SAB)d∣∣AB⇒IJ∣∣AB⇒OJ∣∣(SAB)
⇒(���)∣∣(���)⇒��∣∣(���)⇒(OIJ)∣∣(SAB)⇒IJ∣∣(SAB)

Đáp án B
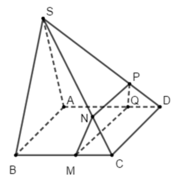
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B

Bài này ứng dụng 1 phần cách giải của bài này:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
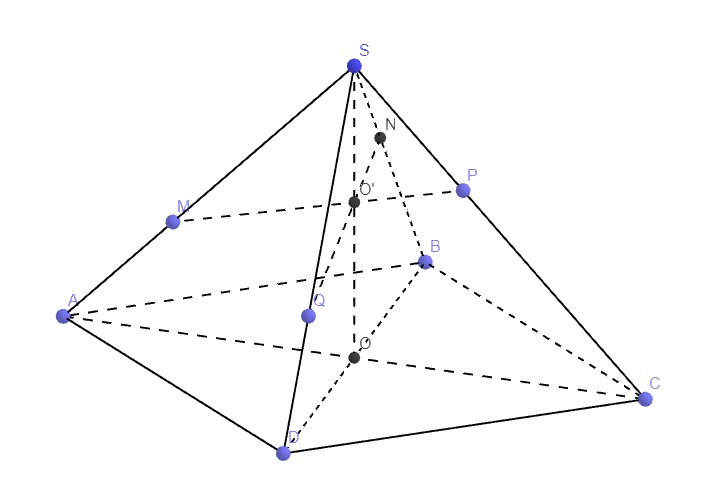
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

bn ơi K thuộc SD hả ? ... nếu vậy thì MK sẽ không thể song song với mặt phẳng ( SBC) đâu nhé :)

a.
\(MN\) là đường trung bình của tam giác ABD \(\Rightarrow MN//BD\Rightarrow MN//\left(SBD\right)\)
b.
\(\dfrac{SI}{SM}=\dfrac{SJ}{SN}\Rightarrow IJ//MN\) (Talet đảo)
Mà \(MN//\left(SBD\right)\Rightarrow IJ//\left(SBD\right)\)
c.
Gọi P là trung điểm IJ, Q là trung điểm MN \(\Rightarrow\) Q đồng thời là trung điểm AO
\(\Rightarrow\dfrac{SP}{SQ}=\dfrac{SI}{SM}=\dfrac{2}{3}\Rightarrow P\) là trọng tâm SAO
Gọi K là trung điểm SA \(\Rightarrow OP\) đi qua K
\(\Rightarrow K\in\left(IJO\right)\)
Mà K là trung điểm SA, O là trung điểm AC \(\Rightarrow KO\) là đường trung bình SAC
\(\Rightarrow SC//KO\Rightarrow SC//\left(IJO\right)\)
Dạ cho em hỏi là bài này anh( chị) có bt cách giải chưa Dạ, chỉ em với