Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn ơi K thuộc SD hả ? ... nếu vậy thì MK sẽ không thể song song với mặt phẳng ( SBC) đâu nhé :)

a.
Ta có: \(\begin{cases}S\in\left(SAB\right)\cap\left(SCD\right)\\ AB\Vert CD\\ AB\subset\left(SAB\right);CD\subset\left(SCD\right)\end{cases}\)
\(\Rightarrow\left(SAB\right)\cap\left(SCD\right)=Sx\Vert AB\Vert CD\)
b.
Gọi O là giao điểm AC và BD =>O là trung điểm AC và BD
\(O\in AC\subset\left(IAC\right)\Rightarrow IO\subset\left(IAC\right)\)
O là trung điểm BD, I là trung điểm SD =>OI là đường trung bình tam giác SBD
=>OI song song SB
Ta có: \(\begin{cases}C\in\left(IAC\right)\cap\left(SBC\right)\\ OI\Vert SB\\ OI\subset\left(IAC\right);SB\subset\left(SBC\right)\end{cases}\) \(\Rightarrow\left(IAC\right)\cap\left(SBC\right)=Cx\Vert SB\)
Đề bài:
Cho hình chóp \(S . A B C D\) có đáy là hình bình hành.
- Tìm giao tuyến của mặt phẳng \(\left(\right. S A B \left.\right)\) và mặt phẳng \(\left(\right. S C D \left.\right)\).
- Gọi \(I\) là trung điểm của \(S D\). Mặt phẳng \(\left(\right. I A C \left.\right)\) và mặt phẳng \(\left(\right. S B C \left.\right)\) cắt nhau theo giao tuyến \(C x\). Chứng minh rằng \(C x \parallel S B\).
Phần a) Tìm giao tuyến của mặt phẳng \(\left(\right. S A B \left.\right)\) và mặt phẳng \(\left(\right. S C D \left.\right)\):
1. Mô tả các mặt phẳng:
- Mặt phẳng \(\left(\right. S A B \left.\right)\) là mặt phẳng chứa các điểm \(S\), \(A\), và \(B\).
- Mặt phẳng \(\left(\right. S C D \left.\right)\) là mặt phẳng chứa các điểm \(S\), \(C\), và \(D\).
2. Tính giao tuyến của hai mặt phẳng:
Hai mặt phẳng này có giao tuyến là một đường thẳng, và để tìm giao tuyến này, ta cần tìm một điểm chung của hai mặt phẳng và một hướng của đường thẳng giao tuyến.
- Mặt phẳng \(\left(\right. S A B \left.\right)\) chứa các điểm \(S\), \(A\), và \(B\).
- Mặt phẳng \(\left(\right. S C D \left.\right)\) chứa các điểm \(S\), \(C\), và \(D\).
Lưu ý rằng điểm \(S\) là chung của cả hai mặt phẳng. Giao tuyến của hai mặt phẳng này sẽ là đường thẳng đi qua điểm \(S\)và vuông góc với các cạnh của đáy \(A B C D\) tại các điểm \(A\), \(B\), \(C\), và \(D\).
Do đáy \(A B C D\) là hình bình hành, các cạnh đối diện của hình bình hành sẽ song song. Do đó, giao tuyến của hai mặt phẳng \(\left(\right. S A B \left.\right)\) và \(\left(\right. S C D \left.\right)\) chính là đoạn thẳng nối giữa hai điểm \(B\) và \(C\) trong không gian.
Kết luận: Giao tuyến của hai mặt phẳng \(\left(\right. S A B \left.\right)\) và \(\left(\right. S C D \left.\right)\) là đoạn thẳng \(B C\).
Phần b) Chứng minh \(C x \parallel S B\):
1. Mô tả các mặt phẳng:
- \(I\) là trung điểm của đoạn \(S D\), nghĩa là \(I\) chia đoạn \(S D\) thành hai phần bằng nhau.
- Mặt phẳng \(\left(\right. I A C \left.\right)\) chứa các điểm \(I\), \(A\), và \(C\).
- Mặt phẳng \(\left(\right. S B C \left.\right)\) chứa các điểm \(S\), \(B\), và \(C\).
Cả hai mặt phẳng này giao nhau tại đường thẳng \(C x\), và chúng ta cần chứng minh rằng đường thẳng \(C x\) song song với \(S B\).
2. Tính chất của các mặt phẳng:
- Mặt phẳng \(\left(\right. I A C \left.\right)\) và mặt phẳng \(\left(\right. S B C \left.\right)\) cắt nhau theo đường thẳng \(C x\).
- Do \(I\) là trung điểm của \(S D\), ta có \(S I = I D\). Vì vậy, \(I\) chia đoạn \(S D\) thành hai phần bằng nhau.
- Mặt phẳng \(\left(\right. I A C \left.\right)\) đi qua \(I\), \(A\), và \(C\), còn mặt phẳng \(\left(\right. S B C \left.\right)\) đi qua \(S\), \(B\), và \(C\).
3. Chứng minh tính song song:
- Ta có thể áp dụng các tính chất về đường thẳng và mặt phẳng song song trong không gian.
- Vì \(I\) là trung điểm của \(S D\), và \(C x\) là giao tuyến của hai mặt phẳng \(\left(\right. I A C \left.\right)\) và \(\left(\right. S B C \left.\right)\), ta nhận thấy rằng đường thẳng \(C x\) phải song song với đường thẳng \(S B\) do tính chất của các mặt phẳng giao nhau tại điểm \(C x\).
Cụ thể, vì hai mặt phẳng \(\left(\right. I A C \left.\right)\) và \(\left(\right. S B C \left.\right)\) có một điểm chung là \(C\) và đường thẳng \(C x\) là giao tuyến của chúng, mà mặt phẳng \(\left(\right. S B C \left.\right)\) chứa \(S B\), do đó \(C x\) sẽ song song với \(S B\).
Kết luận: Đường thẳng \(C x\) song song với \(S B\), tức là \(C x \parallel S B\).
Tóm lại:
- Giao tuyến của mặt phẳng \(\left(\right. S A B \left.\right)\) và mặt phẳng \(\left(\right. S C D \left.\right)\) là đoạn thẳng \(B C\).
- Đường thẳng giao tuyến \(C x\) của hai mặt phẳng \(\left(\right. I A C \left.\right)\) và \(\left(\right. S B C \left.\right)\) song song với \(S B\), tức là \(C x \parallel S B\).

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

Chà, bài này dựng xong hình là xong thôi (tính toán đơn giản bằng Talet)
Đầu tiên là dựng mp qua M và song song (SBD): qua M kẻ các đường thẳng song song SB, SD lần lượt cắt AB, AD tại E và F
Nối EF kéo dài cắt BC tại I và CD tại G
Qua G kẻ đường thẳng song song MF (hoặc SD) cắt MI kéo dài tại J
Talet cho ta: \(\dfrac{MI}{MJ}=\dfrac{IF}{GF}\)
Mà \(\dfrac{GF}{GI}=\dfrac{DF}{BI}=\dfrac{\dfrac{1}{2}AD}{BC+\dfrac{1}{2}BC}=...\)
Vậy là xong

Câu 1:
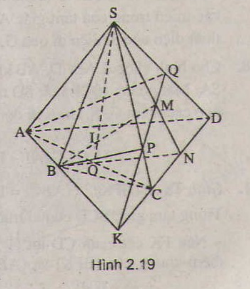
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
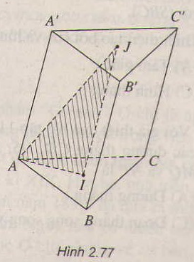
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
Câu 4:
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
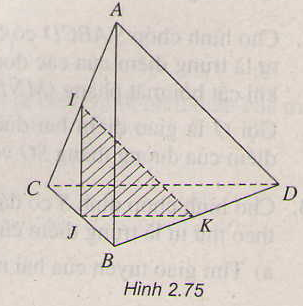
Câu 5:
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy






Đáp án C
Xét mặt phẳng (SAB) và (SCD) có:
S là điểm chung
AB // CD
⇒ Giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và song song với AB