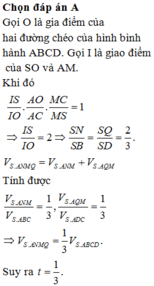Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
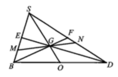
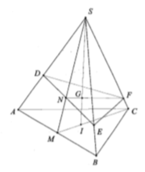
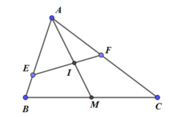
∆ ABC có AM là trung tuyến, I là điểm bất kì trên đoạn AM, đường thẳng đi qua I cắt AB, AC lần lượt tại E, F.
Khi đó: 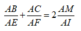
Cách giải:
Ta có: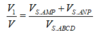
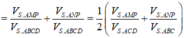

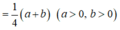
Xét
∆
SAC có: ![]()
![]()
![]()
![]()
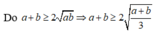
![]()
![]()
Dấu "=" xảy ra 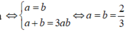
Khi đó 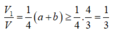
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3 khi và chỉ khi a= b = 2 3
Chọn A.

Đáp án D
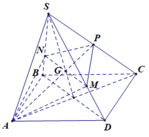
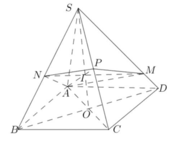
Gọi G là trọng tâm tam giác S A C ⇒ M N đi qua G
Với x = S N S B ; y = S M S D
![]()
![]()
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3

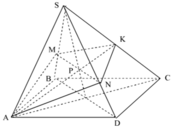
) Gọi P là tr/điểm AS
=> SA v/góc BP (t/giác SAB đêu)
SA v/góc BM =>SA v/góc (BPM)
Gọi P, Q lần lượt là tr/điểm AS và AJ
=> PQ là đ/t/bình t/giác ASJ
=> SJ // PQ. Mặt khác, t/giác SAJ có:
vuông tại S
=> AS v/góc SJ => AS v/góc PQ
Lại có: AS v/góc BP (t/giác SAB đều) => AS v/góc (BPQ) => AS v/góc BQ, lúc đó M là giao điểm BQ và CD.
AB // JM => . Trong t/giác vuông ADM có: