Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

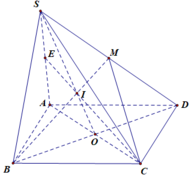
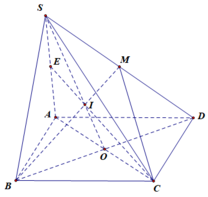
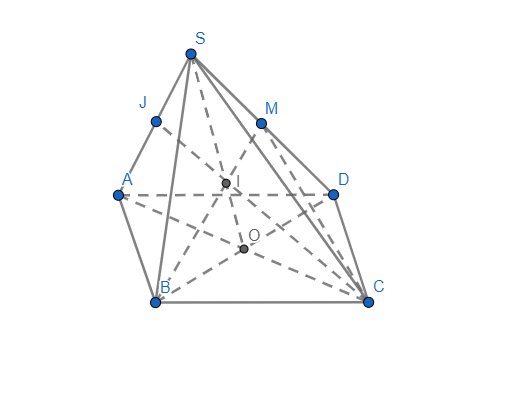
Trong mp(ABCD), gọi \(O=AC\cap BD\)
a) Ta có:
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\)\(\Rightarrow S\in\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}O\in BD\subset\left(SBD\right)\\O\in AC\subset\left(SAC\right)\end{matrix}\right.\)\(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp(SBD), gọi \(I=SO\cap BM\Rightarrow I=BM\cap\left(SAC\right)\)
Ta có: \(\left\{{}\begin{matrix}SM=DM\\OB=OD\end{matrix}\right.\)\(\Rightarrow\dfrac{IB}{IM}=2\)
b) Ta có:
\(\left\{{}\begin{matrix}I\in SO\subset\left(SAC\right)\\I\in BM\subset\left(MBC\right)\end{matrix}\right.\)\(\Rightarrow I\in\left(SAC\right)\cap\left(MBC\right)\)
\(\left\{{}\begin{matrix}C\in\left(SAC\right)\\C\in\left(MBC\right)\end{matrix}\right.\)\(\Rightarrow C\in\left(SAC\right)\cap\left(MBC\right)\)
\(\Rightarrow IC=\left(SAC\right)\cap\left(MBC\right)\)
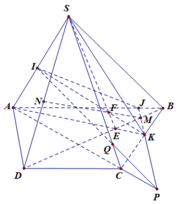
Trong mp(SAC), gọi \(J=SA\cap IC\)\(\Rightarrow J=SA\cap\left(MBC\right)\)
Theo định lý Menelaus, ta có:
\(\dfrac{JS}{JA}.\dfrac{CA}{CO}.\dfrac{IO}{SO}=1\)\(\Rightarrow\dfrac{JS}{JA}.2.\dfrac{1}{3}=1\Leftrightarrow\dfrac{JS}{JA}=\dfrac{3}{2}\)

\(\Rightarrow\dfrac{OC}{CA}=\dfrac{CI}{CS}\Rightarrow OI\) // \(SA\)
\(OI\subset\left(BID\right)\Rightarrow SA\) // \(\left(BID\right)\)
Nếu thêm phần d là : xác định giao điểm K của BG và (SAC).Tính KB/KG thì làm kiểu gì ạ?

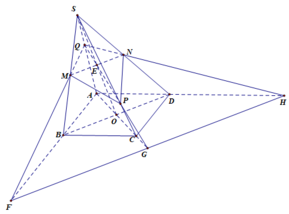
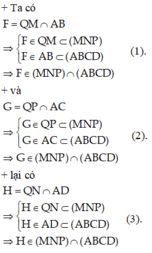
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.