Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

À, tưởng dài mà thực ra cũng dễ thôi, vì toàn điểm đặc biệt cả.
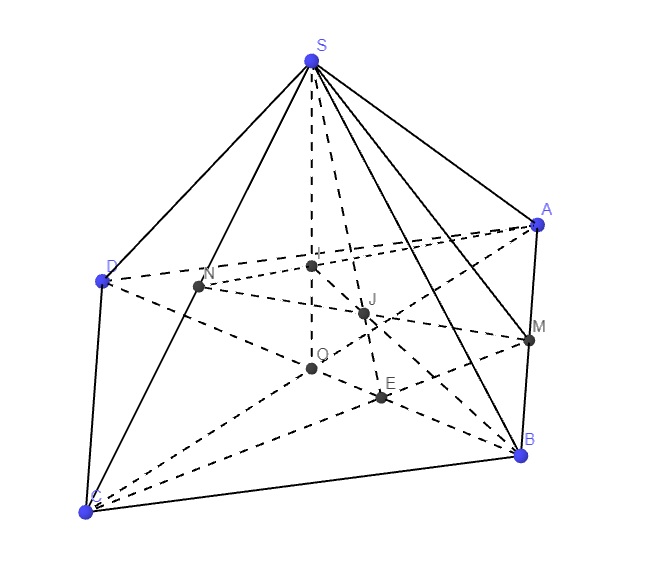
Gọi O là tâm đáy \(\Rightarrow I\) là giao AN và SO
\(\Rightarrow I\) là trọng tâm SAC \(\Rightarrow\dfrac{SI}{SO}=\dfrac{2}{3}\)
Gọi E là giao điểm CM và BD, trong mp (SCM) nối MN cắt SE tại J
E là trọng tâm ABC \(\Rightarrow\dfrac{BE}{BO}=\dfrac{2}{3}\)
Menelaus tam giác BOI:
\(\dfrac{BE}{EO}.\dfrac{OS}{SI}.\dfrac{IJ}{JB}=1\Rightarrow2.\dfrac{3}{2}.\dfrac{IJ}{JB}=1\Rightarrow JB=3IJ\)
\(\Rightarrow IB-IJ=3IJ\Rightarrow\dfrac{IB}{IJ}=4\)

a: Gọi O là giao điểm của AC và BD
Chọn mp(SAC) có chứa AN
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi I là giao điểm của SO với AN
=>I là giao điểm của AN với mp(SBD)
Chọn mp(AMN) có chứa MN
\(B\in AM\subset\left(AMN\right)\)
\(B\in BD\subset\left(SBD\right)\)
Do đó: \(B\in\left(AMN\right)\cap\left(SBD\right)\)
mà \(I\in\left(AMN\right)\cap\left(SBD\right)\)
nên (AMN) giao (SBD)=BI
Gọi K là giao điểm của BI với MN
=>K là giao điểm của MN với mp(SBD)
b: K là giao điểm của BI với MN
=>B,I,K thẳng hàng
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC và O là trung điểm của BD
Xét ΔSAC có
O,N lần lượt là trung điểm của CA,CS
=>ON là đường trung bình
=>ON//SA và ON=SA/2
Xét ΔINO và ΔIAS có
\(\widehat{INO}=\widehat{IAS}\)
\(\widehat{NIO}=\widehat{AIS}\)
Do đó: ΔINO đồng dạng với ΔIAS
=>\(\dfrac{IN}{IA}=\dfrac{NO}{AS}=\dfrac{1}{2}\)

Chứng minh B, J, I thẳng hàng. Áp dụng định lí Mê-nê-la-uýt vào tam giác IAB ta được IJ/JB = 1/4.
Đáp án C

Trong mặt phẳng (SAC) : AF ∩S O = I là trọng tâm tam giác SBD ⇒ IA/IF=2
Đáp án B

a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK

Chọn mp(SAC) có chứa AM
(SAC) giao (SBD)=SO
=>I=AM giao SO

1.
Gọi \(O=AC\cap BD\)
\(AM\in\left(SAC\right)\)
Mà \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(\Rightarrow J=AM\cap SO\)
Qua M kẻ \(d//AB\Rightarrow N=d\cap SD\)

Gọi giao của AC và BD là O
\(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\Leftrightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\Leftrightarrow S\in\left(SAC\right)\cap\left(SBD\right)\)
=>(SAC) giao (SBD)=SO

a.
\(MN\) là đường trung bình của tam giác ABD \(\Rightarrow MN//BD\Rightarrow MN//\left(SBD\right)\)
b.
\(\dfrac{SI}{SM}=\dfrac{SJ}{SN}\Rightarrow IJ//MN\) (Talet đảo)
Mà \(MN//\left(SBD\right)\Rightarrow IJ//\left(SBD\right)\)
c.
Gọi P là trung điểm IJ, Q là trung điểm MN \(\Rightarrow\) Q đồng thời là trung điểm AO
\(\Rightarrow\dfrac{SP}{SQ}=\dfrac{SI}{SM}=\dfrac{2}{3}\Rightarrow P\) là trọng tâm SAO
Gọi K là trung điểm SA \(\Rightarrow OP\) đi qua K
\(\Rightarrow K\in\left(IJO\right)\)
Mà K là trung điểm SA, O là trung điểm AC \(\Rightarrow KO\) là đường trung bình SAC
\(\Rightarrow SC//KO\Rightarrow SC//\left(IJO\right)\)