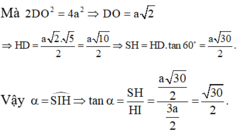Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) ; mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\)
\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\)
\(\left\{{}\begin{matrix}AH\perp\left(SBC\right)\Rightarrow AH\perp SC\\AK\perp\left(SCD\right)\Rightarrow AK\perp SC\end{matrix}\right.\) \(\Rightarrow SC\perp\left(AHK\right)\Rightarrow SC\perp HK\)
Mặt khác theo tính đối xứng hình vuông \(\Rightarrow HK||BD\Rightarrow HK\perp AC\Rightarrow HK\perp\left(SAC\right)\)
\(AI\in\left(SAC\right)\Rightarrow HK\perp AI\)

1.
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông tại D
b.
Do H là trung điểm AD, K là trung điểm SA
\(\Rightarrow KH\) là đường trung bình tam giác SAD
\(\Rightarrow KH||SD\Rightarrow KH||\left(SCD\right)\)
H là trung điểm AD, M là trung điểm BC \(\Rightarrow HM||CD\)
\(\Rightarrow HM||\left(SCD\right)\)
Mà HM cắt KH tại H
\(\Rightarrow\left(HKM\right)||\left(SCD\right)\)
c.
Qua K kẻ đường thẳng song song AB cắt SB tại N
\(\Rightarrow N=\left(HKM\right)\cap SB\)
\(\left\{{}\begin{matrix}KN||AB\\HM||AB\end{matrix}\right.\) \(\Rightarrow KN||HM\) (1)
Mặt khác \(\left\{{}\begin{matrix}HM||CD\\CD||\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM\perp KH\) (2)
(1);(2) \(\Rightarrow\) HKNM là hình thang vuông

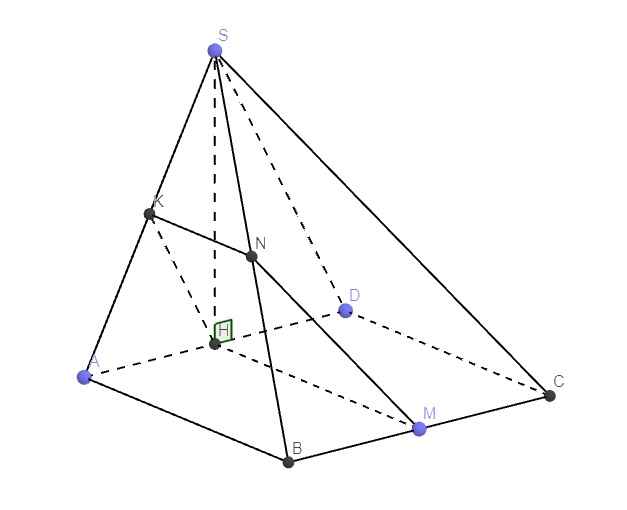
Do O là giao điểm 2 đường chéo \(\Rightarrow\) O là trung điểm AC và BD
Tam giác SAC cân tại S \(\Rightarrow SO\) là trung tuyến đồng thời là đường cao
\(\Rightarrow SO\perp AC\) (1)
Tương tự ta có \(SO\perp BD\) (2)
(1); (2) \(\Rightarrow SO\perp\left(ABCD\right)\)
b. Ta có \(AC\perp BD\) nên tam giác OBC vuông tại O
\(\Rightarrow OE=BE=\dfrac{1}{2}BC\) (trung tuyến ứng với cạnh huyền)
Mà \(\widehat{BCD}=\widehat{BAD}=60^0\Rightarrow\Delta BCD\) đều
\(\Rightarrow BD=BC\Rightarrow OB=BE=\dfrac{1}{2}BC\Rightarrow OB=OE=BE\)
\(\Rightarrow\Delta OBE\) đều \(\Rightarrow OF\perp BC\) (trung tuyến tam giác đều đồng thời là đường cao)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOF\right)\Rightarrow\left(SBC\right)\perp\left(SOF\right)\)

a) Ta có:
\(SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot CB\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AB \bot CB\)
\( \Rightarrow CB \bot \left( {SAB} \right)\)
\(SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot CD\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AD \bot CD\)
\( \Rightarrow CD \bot \left( {SAD} \right)\)
b) Ta có:
\(\left. \begin{array}{l}CB \bot \left( {SAB} \right) \Rightarrow CB \bot AH\\AH \bot SB\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)
\(\left. \begin{array}{l}CD \bot \left( {SAD} \right) \Rightarrow CD \bot AK\\AK \bot SD\end{array} \right\} \Rightarrow AK \bot \left( {SC{\rm{D}}} \right) \Rightarrow AK \bot SC\)
\( \Rightarrow SC \bot \left( {AHK} \right) \Rightarrow SC \bot HK\)
\(\begin{array}{l}\Delta SAB = \Delta SA{\rm{D}}\left( {c.g.c} \right) \Rightarrow SH = SK,SB = S{\rm{D}}\\\left. \begin{array}{l} \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{S{\rm{D}}}} \Rightarrow HK\parallel B{\rm{D}}\\SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot B{\rm{D}}\end{array} \right\} \Rightarrow SA \bot HK\end{array}\)
\(\left. \begin{array}{l}SC \bot HK\\SA \bot HK\end{array} \right\} \Rightarrow HK \bot \left( {SAC} \right) \Rightarrow HK \bot AI\)