K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên





Lời giải:
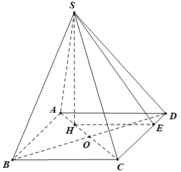
Gọi \(SH\) là đường cao của hình chóp
Từ \(H\) kẻ \(HK\perp AB\). Áp dụng định lý Thales cho tam giác $ABC$ suy ra \(\frac{HK}{BC}=\frac{AH}{AC}=\frac{3}{4}\Rightarrow HK=\frac{3}{4}a\)
Có: \(((SAB),(ABCD))=\angle HKS=60^0\Rightarrow \frac{HS}{HK}=\tan 60\Rightarrow SH=\frac{3\sqrt{3}}{4}a\)
Do đó mà \(V=\frac{1}{3}.SH.S_{ABCD}=\frac{\sqrt{3}}{4}a^3\)