Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
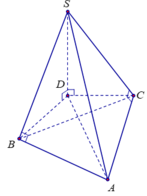
Gọi D là hình chiếu của S lên mặt phẳng (ABC), suy ra S D ⊥ A B C .
Ta có S D ⊥ A B và S B ⊥ A B ( g t ) , suy ra A B ⊥ S B D ⇒ B A ⊥ B D .
Tương tự có A C ⊥ D C hay tam giác ACD vuông ở C.
Dễ thấy ∆ S B A = ∆ S C A (cạnh huyền và cạnh góc vuông), suy ra SB=SC. Từ đó ta chứng minh được ∆ S B D = ∆ S C D nên cũng có DB=DC.
Vậy DA là đường trung trực của BC, nên cũng là đường phân giác của góc B A C ^ .
Ta có
D
A
C
^
=
30
o
, suy ra
D
C
=
a
3
. Ngoài ra góc giữa hai mặt phẳng (SAB) và (ABC) là
S
B
D
^
=
60
o
suy ra
tan
S
B
D
^
=
S
D
B
D
⇒
S
D
=
B
D
tan
S
B
D
^
=
a
3
.
3
=
a
Vậy
V
S
.
A
B
C
=
1
3
.
S
∆
A
B
C
.
S
D
=
1
3
a
2
3
4
.
a
=
a
3
3
12

Chọn C
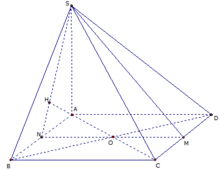
Gọi N là trung điểm của AB => BC // (SMN)
Suy ra d (BC, SM)=d (BC, (SMN))=d (B, (SMN))=d (A, (SMN)).
Dựng AH vuông góc với SN tại H
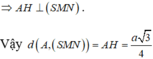
Lại có, trong tam giác vuông SAN:
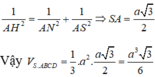

e tưởng chị đăng câu này r
cj tham khảo link này ạ : https://docplayer.vn/193859457-C%C3%A1c-b%C3%A0i-to%C3%A1n-h%C3%ACnh-kh%C3%B4ng-gian-cho-thi-%C4%91%E1%BA%A1i-h%E1%BB%8Dc-1-kh%E1%BB%91i-ch%C3%B3p-b%C3%A0i-1-1-cho-h%C3%ACnh-ch%C3%B3p-s-abcd-c%C3%B3-%C4%91%C3%A1y-abcd-l%C3%A0-h%C3%ACnh-vu%C3%B4ng-c%E1%BA%A1nh-a-tam-gi%C3%A1c-sab-%C4%91%E1%BB%81u-v%C3%A0-sad-9.html