Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

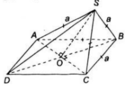
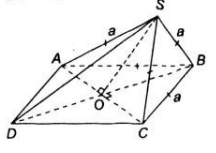
a) Gọi O là tâm của hình thoi, ta có AC ⊥ BD tại O
Vì SA = SC nên SO ⊥ AC.
Do đó AC vuông góc với mặt phẳng (SBD)
Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Ba tam giác SAC, BAC, DAC bằng nhau ( c.c.c) nên ta suy ra OS = OB = OD. Vậy tam giác SBD vuông tại S.

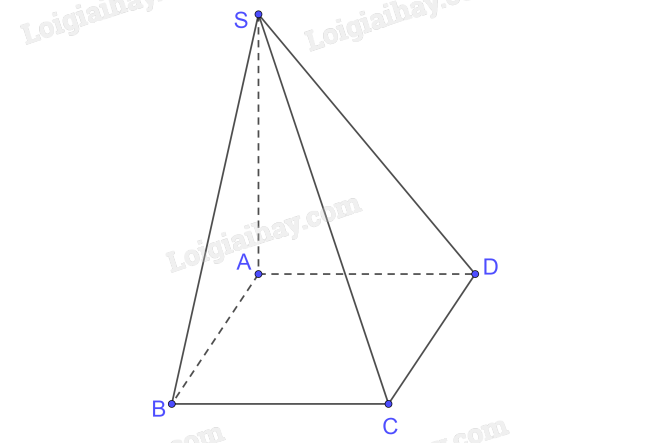
\(\begin{array}{l}\left. \begin{array}{l} + )BC \bot AB\left( {hcn\,\,ABCD} \right)\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AB \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right);SB \subset \left( {SAB} \right) \Rightarrow BC \bot SB\\\left. \begin{array}{l} + )CD \bot AD\left( {hcn\,\,ABCD} \right)\\CD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AD \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow CD \bot SD\end{array}\)
Xét tam giác SAB có
\(SA \bot AB\left( {SA \bot \left( {ABCD} \right)} \right)\)
\( \Rightarrow \) Tam giác SAB vuông tại A
Xét tam giác SBC có
\(SB \bot BC\)
\( \Rightarrow \) Tam giác SBC vuông tại B
Xét tam giác SCD có
\(SD \bot CD\)
\( \Rightarrow \) Tam giác SCD vuông tại D
Xét tam giác SAD có
\(SA \bot AD\left( {SA \bot \left( {ABCD} \right)} \right)\)
\( \Rightarrow \) Tam giác SAD vuông tại A


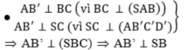
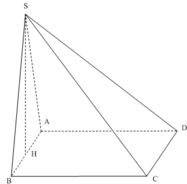


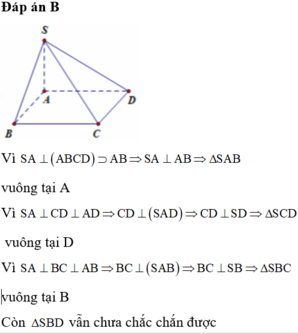

● SA ⊥ (ABCD) ⇒ SA ⊥ AB, SA ⊥ AD.
⇒ Các tam giác SAB, SAD vuông tại A.
● BC ⊥ SA, BC ⊥ AB.
⇒ BC ⊥ SB ⇒ ΔSBC vuông tại B.
● CD ⊥ SA, CD ⊥ AD.
⇒ CD ⊥ SD ⇒ ΔSCD vuông tại D.