

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



S o B H A D G d H' C K
Câu a bạn tự tính nhé!
Câu b: Qua G kẻ đường thẳng d // CD , khoảng cách từ \(d\left(G;\left(SAB\right)\right)=d\left(d;\left(SAD\right)\right)\)
Kẻ HH' vuông CD , nối SH'. Lúc này SH' cách d tại K . \(d\left(K;\left(SAB\right)\right)\) là khoảng cách cần tìm.
Ta có: SH'AB =\(\frac{1}{2}S_{ABCD}\)=\(\frac{1}{2}\times2\sqrt{3}a^2=\sqrt{3}a^2\) \(\Rightarrow HH'=\frac{\sqrt{3}a^2}{a}=\sqrt{3}a\)
Vì K nằm trên d nên \(d\left(K;\left(SAB\right)\right)=\frac{2}{3}HH'=\frac{2\sqrt{3}a}{3}\)

S B N M C D I K A
Gọi I là trung điểm của đoạn AB \(\Rightarrow SI\perp AB,\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SI\perp\left(ABCD\right)\)
Nên \(\widehat{SCI}=\left(\widehat{SC,\left(ABCD\right)}\right)=60^0,CI=\frac{a\sqrt{3}}{2}\Rightarrow SI=CI\tan60^0=\frac{3a}{2}\)
Gọi M là trung điểm của đoạn BC, N là trung điểm đoạn BM
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow IN=\frac{a\sqrt{3}}{4}\)
Ta có : \(S_{ABCD}=2S_{\Delta ABC}=\frac{a^2\sqrt{3}}{2}\Rightarrow V_{S.ABCD}=\frac{1}{3}.\frac{a^2\sqrt{3}}{2}.\frac{3a}{2}=\frac{a^2\sqrt{3}}{4}\)
Ta có \(BC\perp IN,BC\perp SI\Rightarrow BC\perp\left(SIN\right)\)
Trong mặt phẳng (SIN) kẻ \(IK\perp\left(SN\right),K\in SN\), ta có :
\(\begin{cases}IK\perp SN\\IK\perp BC\end{cases}\) \(\Rightarrow IK\perp\left(SBC\right)\Rightarrow d\left(I,\left(SBC\right)\right)=IK\)
Lại có :
\(\frac{1}{IK^2}=\frac{1}{IS^2}+\frac{1}{IN^2}\Rightarrow IK=\frac{3a\sqrt{13}}{26}\Rightarrow d\left(I,\left(SBC\right)\right)=\frac{3a\sqrt{13}}{26}\)
\(\Rightarrow d\left(A,\left(SBC\right)\right)=\frac{3a\sqrt{13}}{13}\)

S B M H A E N C D
Gọi H là hình chiếu vuông góc của S lên AB, suy ra \(SH\perp\left(ABCD\right)\)
Do đó, SH là đường cao của hình chóp S.BMDN
Ta có : \(SA^2+SB^2=a^2+3a^2=AB^2\)
Nên tam giác SAB là tam giác vuông tại S.
Suy ra : \(SM=\frac{AB}{2}=a\) Do đó tam giác SAM là tam giác đều, suy ra \(SH=\frac{a\sqrt{3}}{3}\)
Diện tích của tứ giác BMDN là \(S_{BMDN}=\frac{1}{2}S_{ABCD}=2a^2\)
Thể tích của khối chóp S.BMDN là \(V=\frac{1}{3}SH.S_{BMDN}=\frac{a^3\sqrt{3}}{3}\)
Kẻ ME song song với DN (E thuộc AD)
Suy ra : \(AE=\frac{a}{2}\) Đặt \(\alpha\) là góc giữa 2 đường thẳng SM và DN
Ta có \(\left(\widehat{SM,ME}\right)=\alpha\), theo định lý 3 đường vuông góc ta có \(SA\perp AE\)
Suy ra :
\(SE=\sqrt{SA^2+AE^2}=\frac{a\sqrt{5}}{2};ME=\sqrt{AM^2+AE^2}=\frac{a\sqrt{5}}{2}\)
Tam giác SME là tam giác cân tại E nên \(\begin{cases}\widehat{SME}=\alpha\\\cos\alpha=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\end{cases}\)
Cho mình hỏi, tam giác cân thì tại sao lại suy ra cos góc kia như thế ??


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
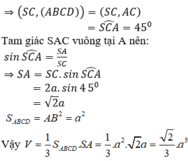

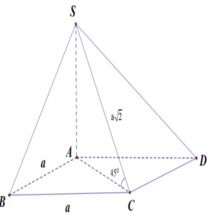
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
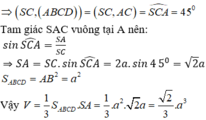

Ta có \(\left(SHC\right)\cap\left(SHD\right)=SH\)
Từ giả thiết \(\left(SHC\right)\perp\left(ABCD\right);\left(SHD\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(\Leftrightarrow V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}AB.AD.SH=\frac{1}{3}a^2\sqrt{3}.SH\left(1\right)\)
Ta có \(SH\perp\left(ABCD\right)\Rightarrow HD\) là hình chiếu của SD trên (ABCD), suy ra góc giữa SD và (ABCD) là \(\widehat{SDH}=60^0\Rightarrow SH=HD\tan\widehat{SDHH}=\frac{a\sqrt{39}}{2}\)
Khi đó \(V_{S.ABCD}=\frac{1}{2}a^3\sqrt{13}\)
Dựng hình bình hành ACBE. Khi đó AC//BE suy ra AC//(SBE)
\(\Rightarrow d\left(AC,SB\right)=d\left(AC,\left(SBE\right)\right)=d\left(A,\left(SBE\right)\right)=2d\left(H,\left(SBE\right)\right)\)
Gọi K, I lần lượt là hình chiếu của H trên BE và SK.
Khi đó \(BE\perp KH,BE\perp SH\Rightarrow BE\perp HI\left(1\right)\)
Mặt khác \(HI\perp SK\left(2\right)\)
Từ (1) và (2) suy ra \(HI\perp\left(SBE\right)\Rightarrow d\left(H,\left(SBE\right)\right)=HI\)
Tính được \(HK=\frac{a\sqrt{3}}{4};HI=\frac{a\sqrt{39}}{\sqrt{212}}\)
\(\Rightarrow d\left(AC,SB\right)=2d\left(H,\left(SBE\right)\right)=2HI=\frac{a\sqrt{39}}{\sqrt{53}}=\frac{a\sqrt{2067}}{53}\)

Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà