Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...
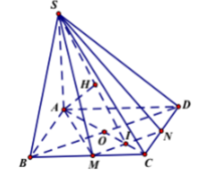
AM là hình chiếu của SM trên (ABCD).
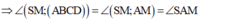
- Xét tam giác vuông ABM ta có: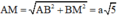 
- Xét tam giác vuông SAM ta có: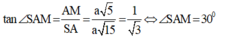 
1: Gọi giao điểm của AC và BD là O trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SO
Xét ΔSDC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔSDC
=>PN//SC
PN//SC
SC\(\subset\)(SBC)
PN không nằm trong mp(SBC)
Do đó: PN//(SBC)
1: Trong mp(ABCD), gọi O là giao điểm của AC và BD
O∈AC⊂(SAC)
O∈BD⊂(SBD)
Do đó: O∈(SAC) giao (SBD)(1)
S∈(SAC)
S∈(SBD)
Do đó: S∈(SAC) giao (SBD)(2)
Từ (1),(2) suy ra (SAC) giao (SBD)=SO
Xét ΔDSC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔDSC
=>PN//SC
mà SC⊂(SBC)
nên PN//(SBC)
2: Chọn mp(SAD) có chứa SA
P∈SD⊂(SAD)
P∈(MNP)
Do đó: P∈(SAD) giao (MNP)(3)
Trong mp(ABCD), gọi K là giao điểm của MN và AD
K∈MN⊂(MNP)
K∈AD⊂(SAD)
DO đó: K∈(SAD) giao (MNP)(4)
Từ (3),(4) suy ra (SAD) giao (MNP)=PK
Gọi Q là giao điểm của PK và SA
=>Q là giao điểm của (MNP) và SA
Xét ΔNCM và ΔNDK có
\(\hat{NCM}=\hat{NDK}\) (hai góc so le trong, DK//MC)
NC=ND
\(\hat{CNM}=\hat{DNK}\) (hai góc đối đỉnh)
Do đó: ΔNCM=ΔNDK
=>CM=DK
=>\(DK=\frac12BC=\frac12DA\)
=>\(KD=\frac13KA\)
Theo Meneleus, ta có:
\(\frac{KD}{KA}\cdot\frac{QA}{QS}\cdot\frac{PS}{PD}=1\)
=>\(\frac13\cdot\frac{QA}{QS}\cdot1=1\)
=>\(\frac{QA}{QS}=1:\frac13=3\)
=>QA=3QS
SQ+QA=SA
=>SA=SQ+3SQ=4SQ
=>\(\frac{SQ}{SA}=\frac14\)
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
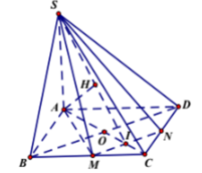
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
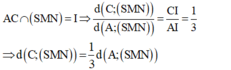
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
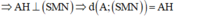
- Ta có:
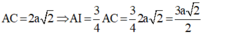
- Xét tam giác vuông SAI ta có:
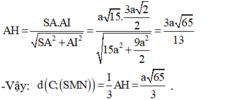
1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)
a, \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\O\subset\left(SAC\right)\end{matrix}\right.\Rightarrow SO\subset\left(SAC\right)\)
\(\left\{{}\begin{matrix}S\subset\left(SBD\right)\\O\subset\left(SBD\right)\end{matrix}\right.\Rightarrow SO\subset\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Gọi \(K=AD\cap BC\)
\(\Rightarrow\left\{{}\begin{matrix}S\subset\left(SAD\right)\\K\subset\left(SAD\right)\end{matrix}\right.\Rightarrow SK\subset\left(SAD\right)\)
\(\left\{{}\begin{matrix}S\subset\left(SBC\right)\\K\subset\left(SBC\right)\end{matrix}\right.\Rightarrow SK\subset\left(SBC\right)\)
\(\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
Ta có: