Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6)
Đáp án A
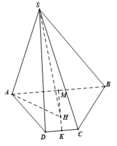
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) 
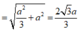
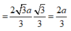
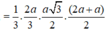
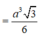
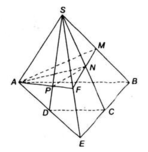
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
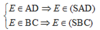
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.
a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD
a. Em kiểm tra lại đề bài xem có nhầm lẫn đâu không.
Ta có CN cắt AB tại N (do N là trung điểm AB) nên không tồn tại \(d\left(CN,AB\right)\) (chỉ có khoảng cách giữa 2 đường thẳng song song hoặc chéo nhau chứ không có khoảng cách giữa 2 đường thẳng cắt nhau).
b.
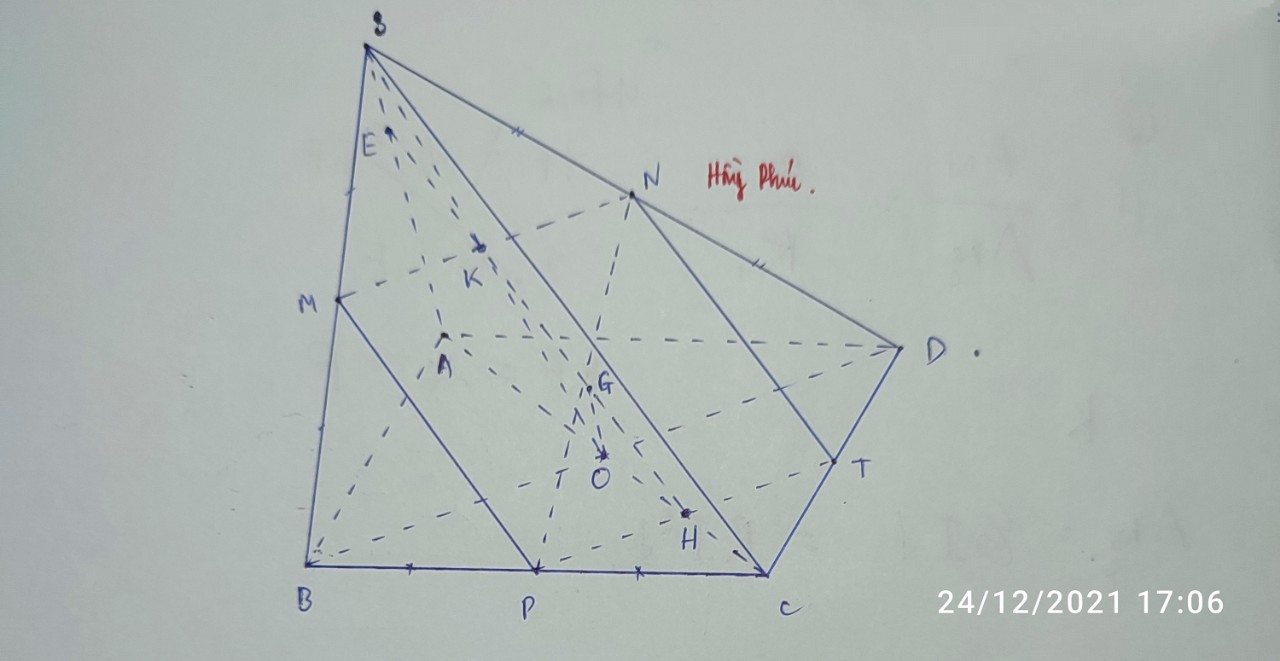
Gọi E là điểm đối xứng D qua A \(\Rightarrow DE=2AD=2BC\), gọi F là trung điểm SE.
\(\Rightarrow MF\) là đường trung bình tam giác SDE \(\Rightarrow\left\{{}\begin{matrix}MF=\dfrac{1}{2}DE=BC\\MF||DE||BC\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác BCMF là hình bình hành \(\Rightarrow CM||BF\)
Lại có AM là đường trung bình tam giác SDE \(\Rightarrow AM||SE\)
\(\Rightarrow\left(ACM\right)||\left(SBE\right)\Rightarrow d\left(SB,CM\right)=d\left(\left(ACM\right),\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Gọi H là trung điểm BE, do \(AE=AD=AB\Rightarrow\Delta ABE\) vuông cân tại A
\(\Rightarrow AH\perp BE\Rightarrow BE\perp\left(SAH\right)\)
Trong mp (SAH), từ A kẻ \(AK\perp SH\) \(\Rightarrow AK\perp\left(SBE\right)\)
\(\Rightarrow AK=d\left(A;\left(SBE\right)\right)=d\left(SB,CM\right)\)
\(AH=\dfrac{1}{2}BE=\dfrac{1}{2}\sqrt{AB^2+AE^2}=\dfrac{a\sqrt{2}}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SAH:
\(AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{a\sqrt{21}}{7}\)
a) △SAB có: M, N là trung điểm của SA, SB nên MN // AB
Mà AB // CD
Suy ra MN // CD mà CD thuộc (SCD)
Do đó: MN // (SCD)
b) Ta có: MN = \(\dfrac{1}{2}\) AB
Mà CD = \(\dfrac{1}{2}\) AB
Suy ra: MN = CD mà MN // CD
Nên MNCD là hình bình hành. Do đó MD // CN
Mà CN thuộc (SBC)
Suy ra: DM // (SBC).
c) Gọi G là giao điểm của DM và AI; H là trung điểm của AB; O là giao điểm của AC và DH
Ta có: AHCD là hình bình hành vì AH // CD, AH = CD
Do đó: O là trung điểm của AC và DH
Ta chứng minh được G là trung điểm của DM
△DMH có: G, O là trung điểm của DM, DH
Suy ra: GO // MH
Mà MH // SB (M, H là trung điểm của SA, AB)
Do đó: GO // SB mà GO thuộc (AIC) nên SB // (AIC).
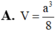
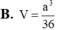
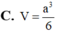
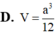
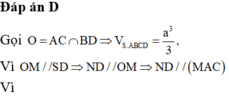
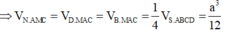
Đáp án B
Ta có: