Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) △SAB có: M, N là trung điểm của SA, SB nên MN // AB
Mà AB // CD
Suy ra MN // CD mà CD thuộc (SCD)
Do đó: MN // (SCD)
b) Ta có: MN = \(\dfrac{1}{2}\) AB
Mà CD = \(\dfrac{1}{2}\) AB
Suy ra: MN = CD mà MN // CD
Nên MNCD là hình bình hành. Do đó MD // CN
Mà CN thuộc (SBC)
Suy ra: DM // (SBC).
c) Gọi G là giao điểm của DM và AI; H là trung điểm của AB; O là giao điểm của AC và DH
Ta có: AHCD là hình bình hành vì AH // CD, AH = CD
Do đó: O là trung điểm của AC và DH
Ta chứng minh được G là trung điểm của DM
△DMH có: G, O là trung điểm của DM, DH
Suy ra: GO // MH
Mà MH // SB (M, H là trung điểm của SA, AB)
Do đó: GO // SB mà GO thuộc (AIC) nên SB // (AIC).

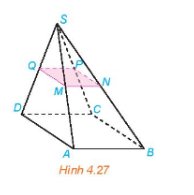
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.
Tương tự ta có: NP // BC, PQ // CD, MQ // AD.
Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.
Như vậy, MNPQ là hình bình hành.


Ta có:MN là đường trung bình của tam giác SAB \(\Rightarrow MN//AB, MN= \frac{1}{2}AB \)
Mà \(\ CD//AB, CD= \frac{1}{2}AB \)
Suy ra: MN//CD, MN = CD.
Từ (1) và (2) suy ra MNCD là hình bình hành
Vậy NC // MD.

Bạn @than thien nếu bạn copy từ AI hay ChatGPT thì hãy xem kỹ các ký tự của bài mình, và khuyên bạn là nên hạn chế sopy AI hay ChatGPT thôi !

tham khảo:

a) Tam giác SAB có MN là đường trung bình nên MN//SA
Mà SA⊥(ABCD) nên MN⊥(ABCD). Suy ra MN⊥AB
Hình thang ABCD có NP là đường trung bình nên NP//BC//AD. Mà BC⊥AB nên NP⊥ABTa có AB vuông góc với hai đường thẳng MN và NP cắt nhau cùng thuộc (MNPQ) nên AB⊥(MNPQ)
b) Vì AB⊥(MNPQ);MQ∈(MNPQ) nên AB⊥MQ
Tam giác SBC có MQ là đường trung bình nên MQ//BC. Mà SA⊥BC nên SA⊥MQ
Ta có MQ vuông góc với hai đường thẳng SA và AB cắt nhau cùng thuộc (SAB) nên MQ⊥(SAB)

Do M là trung điểm SD, N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (1)
Tương tự PQ là đường trung bình tam giác SAB \(\Rightarrow PQ||AB\)
\(\Rightarrow MN||PQ\Rightarrow\) 4 điểm M, N, P, Q đồng phẳng
Lại có MQ là đường trung bình tam giác SAD \(\Rightarrow MQ||AD\)
Mà \(AD\in\left(ABCD\right)\Rightarrow MQ||\left(ABCD\right)\)
Do \(CD\in\left(ABCD\right)\), từ \(\left(1\right)\Rightarrow MN||\left(ABCD\right)\)
Mà \(\left\{{}\begin{matrix}MN\in\left(MNPQ\right)\\MQ\in\left(MNPQ\right)\\MN\cap MQ=M\end{matrix}\right.\)\(\Rightarrow\left(MNPQ\right)||\left(ABCD\right)\)

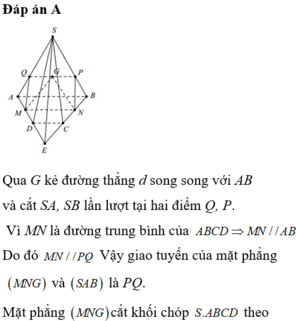




Xét tam giác SAB ta có MN là đường trung bình suy ra MN // AB.
Mà AB // CD do đó MN // CD.
Suy ra MNCD là hình thang.