Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đáy.
Cách giải
S C ; A B C D = S C ; A C = S C A
ABCD là hình vuông cạnh a ⇒ A C = a 2
Xét tam giác vuông SAC có:
tan = S A A C = 2 a a 2 = 2
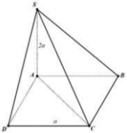

Đáp án A.
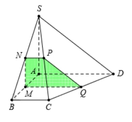
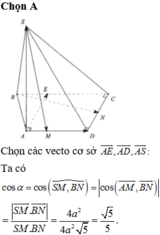
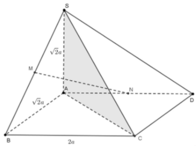
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .

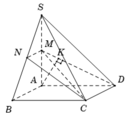
Xác định được ![]()
Vì M là trung điểm SA nên
![]()
Kẻ ![]() và chứng minh được
và chứng minh được ![]() nên
nên ![]()
Trong
∆
vuông MAD tính được ![]()
Chọn A.

Chọn gốc toạ độ tại A. Các tia Ox; Oy; Oz lần lượt trùng với các tia AD, AB, AS ta có tọa độ điểm là A(0;0;0); D(2;0;0); B ( 0 ; 2 ; 0 ) ; S ( 0 ; 0 ; 2 ) ; C 2 ; 2 ; 0 ; M 0 ; 2 2 ; 2 2 ; N 1 ; 0 ; 0
Do vậy
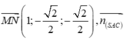
![]()
và
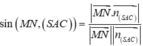
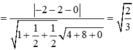
![]()
Chọn đáp án B.
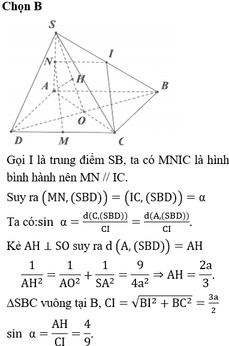
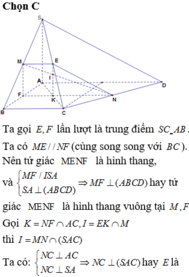




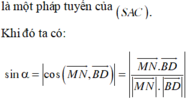
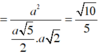

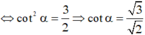

Chọn C