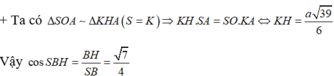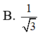Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

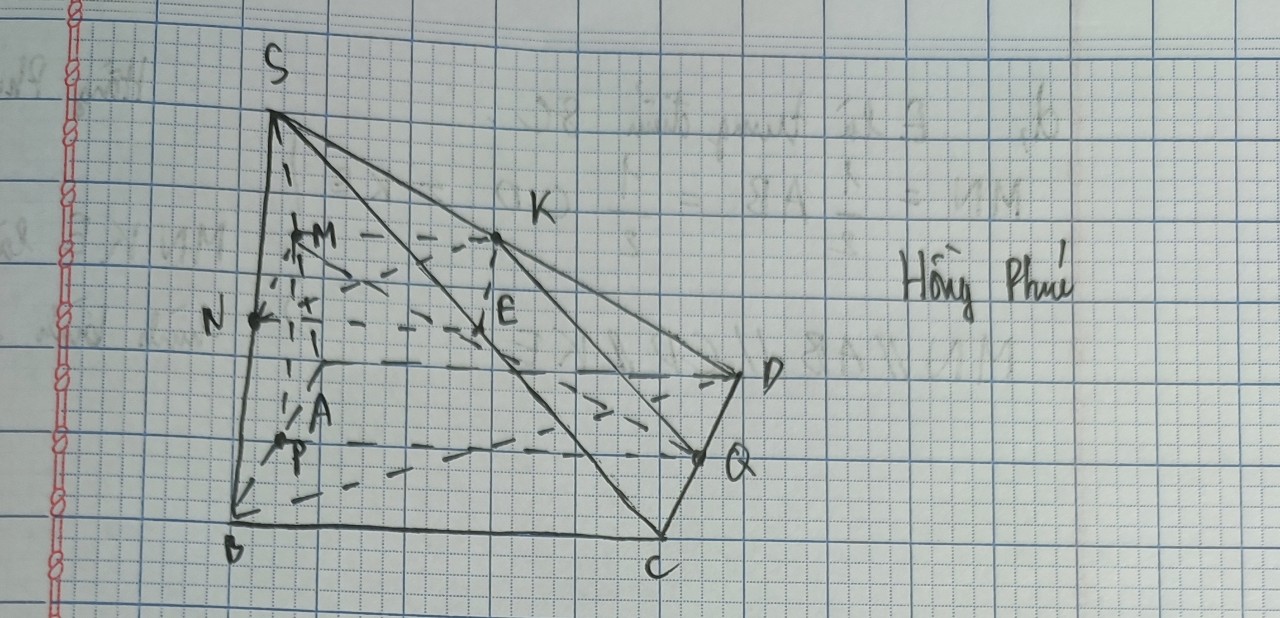
a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
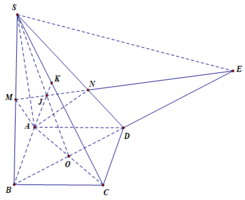
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK

Chọn đáp án A
+ Ta có
![]()
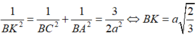
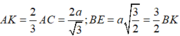
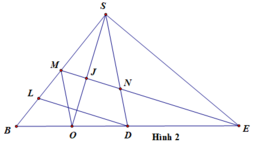
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH