Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)

a.
Do tam giác SAB đều \(\Rightarrow SB=AB=a\)
Trong tam giác SBC ta có:
\(SB^2+BC^2=2a^2=SC^2\)
\(\Rightarrow\Delta SBC\) vuông tại B (pitago đảo)
\(\Rightarrow BC\perp SB\)
Mà \(BC\perp AB\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
Do \(SH\in\left(SAB\right)\Rightarrow BC\perp SH\) (1)
Lại có SAB là tam giác đều, mà SH là đường trung tuyến (H là trung điểm AB)
\(\Rightarrow SH\) đồng thời là đường cao hay \(SH\perp AB\) (2)
(1);(2) \(\Rightarrow SH\perp\left(ABCD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) HM là hình chiếu vuông góc của SM lên (ABCD)
\(\Rightarrow\widehat{SMH}\) là góc giữa SM và (ABCD) hay \(\alpha=\widehat{SMH}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(HM=BC=a\) \(\Rightarrow tan\alpha=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
c.
Do H là trung điểm AB, K là trung điểm AD \(\Rightarrow\) HK là đường trung bình tam giác ABD
\(\Rightarrow HK||BD\)
Mà \(BD\perp AC\) (hai đường chéo hình vuông)
\(\Rightarrow HK\perp AC\) (3)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\) (4)
(3);(4) \(\Rightarrow AC\perp\left(SHK\right)\Rightarrow AC\perp SK\)

Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...

a: (SBD) giao (ABCD)=BD
AB vuông góc BD
SB vuông góc BD
=>góc cần tìm là góc SBA

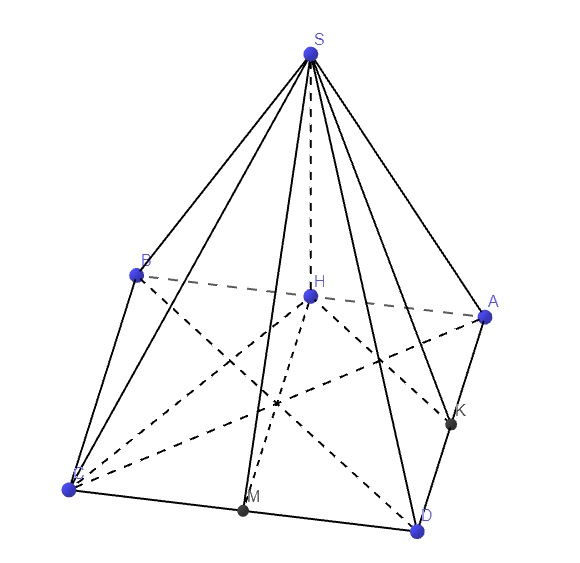
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
M là điểm nào nhỉ?
c.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\HK\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHK\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SCD) và (ABCD)
\(HK=AD=a\Rightarrow tan\widehat{SKH}=\dfrac{SH}{HK}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SKH}=30^0\)
d.
Từ H kẻ \(HE\perp SK\) (E thuộc SK)
\(CD\perp\left(SHK\right)\) theo cmt \(\Rightarrow CD\perp HE\)
\(\Rightarrow HE\perp\left(SCD\right)\Rightarrow HE=d\left(H;\left(SCD\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}\Rightarrow HE=\dfrac{a}{2}\)

a: Qua S kẻ đường Sx song song SD
=>Sx vuông góc SA
SC vuông góc CD
=>SC vuông góc Sx
((SAB);(SCD))=góc ASC
b: (SBD) căt (SAB)=SB
Kẻ DA vuông góc AB
mà DA vuông góc SA
nên DA vuông góc (SAB)
=>DA vuông góc SB
Kẻ AK vuông góc SB
=>((SBD);(SAB))=góc AKD
c: (SBC) giao (SCD)=SC
Kẻ BH vuông góc SC
Qua H kẻ HF//CD
=>HF vuông góc SC
=>((SBC);(SCD))=góc BHF
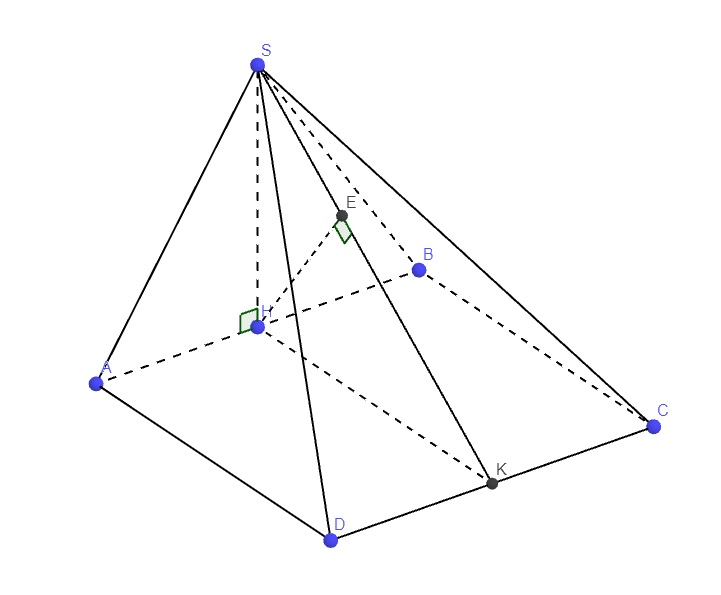
\(AC=AB\sqrt{2}=2a\sqrt{2}\Rightarrow OA=\dfrac{1}{2}AC=a\sqrt{2}\)
\(SO=\sqrt{SA^2-OA^2}=\dfrac{a}{2}\)
O là trung điểm AC, M là trung điểm AB \(\Rightarrow OM\) là đường trung bình tam giác ABC
\(\Rightarrow OM||AB\Rightarrow OM\perp CD\)
Mà \(SO\perp CD\) (chóp đều) \(\Rightarrow CD\perp\left(SOM\right)\Rightarrow CD\perp SM\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\\SO\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow\left(SBD\right)\perp\left(ABCD\right)\)
\(SO\perp\left(ABCD\right)\Rightarrow\) OD là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDO}\) là góc giữa SD là (ABCD)
\(OD=OA=a\sqrt{2}\Rightarrow tan\widehat{SDO}=\dfrac{SO}{OD}=\dfrac{\sqrt{2}}{4}\Rightarrow\widehat{SDO}\approx19^028'\)
\(CD\perp\left(SOM\right)\) theo chứng minh từ câu b
Mà \(CD\in\left(SCD\right)\Rightarrow\left(SCD\right)\perp\left(SOM\right)\)
\(\Rightarrow\) Góc giữa (SOM) và (SCD) bằng 90 độ
góc giữa (SOM) và (SCD) là góc nào vậy ạ?