Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
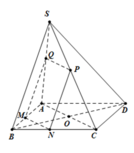
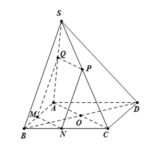
Dễ thấy AB ⊥ BC. Suy ra SB ⊥ BC, ∆ SMN đồng dạng với ∆ SCB, do đó
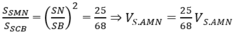

Đáp án D
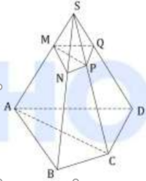

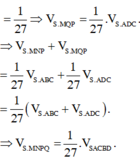
Chú ý: Em nhớ rằng, công thức tính tỉ số thể tích chỉ áp dụng cho khối chóp tam giác. Còn với khối chóp tứ giác, ngũ giác, lục giác,… em cần chia ra thành các khối chóp tam giác và áp dụng công thức.
Công thức giải nhanh:
Cắt khối chóp bởi mặt phẳng song song với đáy: Xét khối chóp S . A 1 A 2 . . . . . A n , mặt phẳng (P) song song với mặt đáy cắt cạnh S A 1 tại m thỏa mãn . Khi đó (P) chia khối chóp thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V' và khối đa diện ban đầu có thể tích V thì V ' V = k 3
Nên ⇒ V S . M N P Q V S . A B C D = 1 3 2 = 1 27

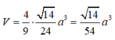

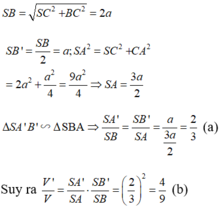
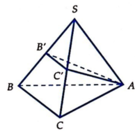

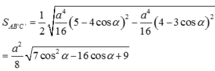
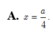
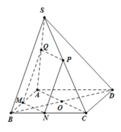
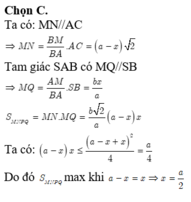
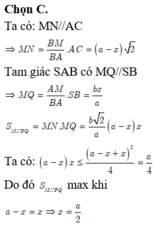
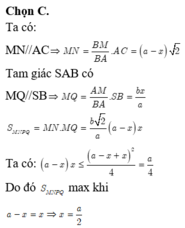
Để xác định vị trí của M để thể tích hình chóp S.A'B'C' đạt giá trị lớn nhất, ta sử dụng nguyên lý cơ sở của hình học không gian. Gọi H là trung điểm của đoạn thẳng BC. Ta có: - Đường thẳng A'H song song với đường thẳng BC. - Đường thẳng B'H song song với đường thẳng AC. - Đường thẳng C'H song song với đường thẳng AB. Do đó, ta có thể xem hình chóp S.A'B'C' là hình chóp đồng dạng với hình chóp S.ABC, tức là các cạnh của chúng có tỉ lệ tương ứng. Vì vậy, để thể tích hình chóp S.A'B'C' đạt giá trị lớn nhất, ta cần chọn M sao cho tỉ lệ giữa độ dài các đoạn thẳng SA', SB', SC' và độ dài các đoạn thẳng SA, SB, SC là nhỏ nhất. Đặt x = SA'/SA = SB'/SB = SC'/SC. Ta cần tìm giá trị của x để x đạt giá trị nhỏ nhất. Áp dụng định lí Thales, ta có: x = SA'/SA = S'A'/S'A = MA'/MA. Vì A'H song song với BC, ta có: MA'/MA = A'H/AH = A'C'/AC. Tương tự, ta có: MA'/MA = A'H/AH = A'B'/AB. Do đó, ta có: x = SA'/SA = SB'/SB = SC'/SC = A'C'/AC = A'B'/AB. Vậy, để x đạt giá trị nhỏ nhất, ta cần chọn M sao cho A'C'/AC = A'B'/AB đạt giá trị nhỏ nhất. Từ đó, ta suy ra M nằm trên đường thẳng A'H, với H là trung điểm của đoạn thẳng BC.