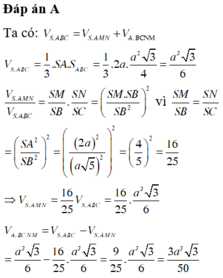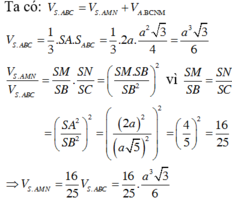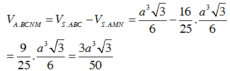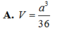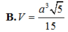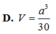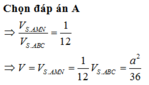Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\dfrac{V_{SAMC}}{V_{SABC}}=\dfrac{SM}{SB}\)
Theo hệ thức lượng: \(SA^2=SM.SB\Rightarrow SM=\dfrac{SA^2}{SB}\)
\(\Rightarrow\dfrac{SM}{SB}=\left(\dfrac{SA}{SB}\right)^2\)
\(\Rightarrow V_{SAMC}=\left(\dfrac{SA}{SB}\right)^2.V\)
2.
Ta có: \(\dfrac{V_{SAMN}}{V_{SABC}}=\dfrac{SN}{SC}.\dfrac{SM}{SB}\)
Theo c/m câu a ta có \(\dfrac{SM}{SB}=\left(\dfrac{SA}{SB}\right)^2\)
Tương tự áp dụng hệ thức lượng cho tam giác vuông SAC:
\(SA^2=SN.SC\Rightarrow SN=\dfrac{SA^2}{SC}\Rightarrow\dfrac{SN}{SC}=\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAMN}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2.V\)

Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
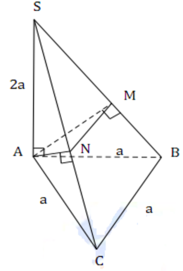
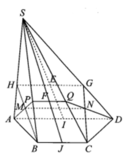
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 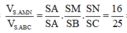
![]()
Do đó ![]()
![]()
Chọn C.

Chọn B

Ta có B C ⊥ S M . Gọi H là hình chiếu vuông góc của A trên SM. Do
![]() và FE đi qua H.
và FE đi qua H.
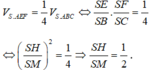
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
⇒ S A = a 3 2 V S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8

Chọn D
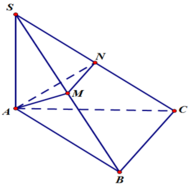
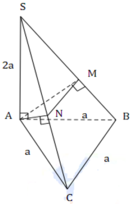
Thể tích khối chóp S. ABC là:
![]()
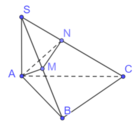
Do SA=AB=AC=a nên các tam giác SAC, SAB cân tại A.
Theo đề bài M, N là hình chiếu của A trên SB, SC nên M, N lần lượt là trung điểm SB, SC.
Khi đó:
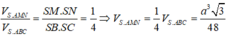
Vậy thể tích khối chóp A. BCNM là: