Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp:
- Chứng minh Δ A B C vuông tại B, tìm tâm và bán kính đường tròn ngoại tiếp tam giác đáy.
- Sử dụng công thức R 2 = h 2 4 + r 2 với R là bán kính hình cầu ngoại tiếp khối chóp, h là chiều cao, r là bán kính đường tròn ngoại tiếp đa giác đáy.
Cách giải:
Ta có: cos 60 ° = 1 2 = a 2 a → cos B A C = A B A C
⇒ Δ A B C vuông tại B.
Gọi M là trung điểm AC.
⇒ M là tâm đường tròn ngoại tiếp Δ A B C
⇒ M A = M A = A C 2 = a

Gọi r là bán kính đường tròn ngoại tiếp tam giác đáy.
R là bán kính mặt cầu ngoại tiếp hình chóp.
h là chiều cao hình chóp.
Ta có công thức sau:
R 2 = h 2 4 + r 2 ⇒ R 2 = a 2 4 + a 2 = a 5 2
⇒ V = 4 3 π R 3 = 5 a 5 6
Chú ý khi giải:
HS cần linh hoạt trong việc chứng minh Δ A B C vuông tại B và biết sử dụng công thức liên hệ giữa R, r, h.

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Chọn đáp án C
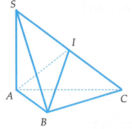
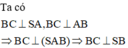
Vậy hai điểm cùng nhìn cạnh dưới một góc vuông. Điều đó chứng tỏ SC là đường kính của mặt cầu ngoại tiếp hình chóp. Do đó bán kính
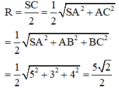

Chọn đáp án D.