Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right),AB \bot BC \Rightarrow BC \bot \left( {SAB} \right),BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)
b) +) Trong (SAC) kẻ \(AD \bot SC \Rightarrow d\left( {A,SC} \right) = AD\)
Xét tam giác ABC vuông tại B có
\(\sin \widehat {CAB} = \frac{{BC}}{{AC}} \Rightarrow AC = \frac{a}{{\sin {{30}^0}}} = 2a\)
Xét tam giác SAC vuông tại A có
\(\frac{1}{{A{D^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow AD = \frac{{2a\sqrt 3 }}{3}\)
Do đó \(d\left( {A,SC} \right) = \frac{{2a\sqrt 3 }}{3}\)
+) \(\left( {SAB} \right) \bot \left( {SBC} \right),\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
Trong (SAB) kẻ \(AE \bot SB\)
\( \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AE\)
Xét tam giác ABC vuông tại B có
\(\tan \widehat {CAB} = \frac{{BC}}{{AB}} \Rightarrow AB = \frac{a}{{\tan {{30}^0}}} = a\sqrt 3 \)
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \frac{5}{{6{a^2}}} \Rightarrow AE = \frac{{a\sqrt {30} }}{5}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt {30} }}{5}\)

a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \tan {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{\sqrt 3 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {SMA} = \arctan \frac{1}{2}\)

Kẻ \(AH \bot BC\left( {H \in BC} \right)\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)
\( \Rightarrow \widehat {SHA} = \alpha \)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)

a) Xét tam giác ABC cân tại A có
AM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) AM là đường cao \( \Rightarrow \) \(AM \bot BC\)
Ta có:
\(\left. \begin{array}{l}AM \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AM \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAM} \right)\)
b) \(\left. \begin{array}{l}BC \bot \left( {SAM} \right)\\SM \subset \left( {SAM} \right)\end{array} \right\} \Rightarrow BC \bot SM\)
Xét tam giác SBC có:
+) SM là đường cao \(\left( {BC \bot SM} \right)\)
+) SM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) Tam giác SBC cân tại S.

a) +) Xét tam giác SBC có
N, P lần lượt là trung điểm SB, SC
\( \Rightarrow \) PN là đường trung bình tam giác SBC
\( \Rightarrow \) PN // BC \( \Rightarrow \) PN // (ABC)
+) Xét tam giác SAB có
N, M lần lượt là trung điểm SB, SA
\( \Rightarrow \) MN là đường trung bình tam giác SAB
\( \Rightarrow \) MN // AB
+) \(\left. \begin{array}{l}PN//BC,MN//AB\\PN \cap MN = \left\{ N \right\},BC \cap AB = \left\{ B \right\}\end{array} \right\} \Rightarrow \left( {MNP} \right)//\left( {ABC} \right)\)
\( \Rightarrow \) d((MNP), (ABC)) = d(M, (ABC)) = MA \( = \frac{{SA}}{2} = \frac{h}{2}\) do SA \( \bot \) (ABC)
+) PN // (ABC) \( \Rightarrow \) d(NP,(ABC)) = d(N,(ABC)) = d(M,(ABC))\( = \frac{h}{2}\) (do MN // (ABC))
b)
Ta có \(SA \bot BC,AB \bot BC \Rightarrow BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
\(\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
(SAB): kẻ \(AH \bot SB\)
\( \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow \) d(A,(SBC)) = AH
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{h^2}{a^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)

a) Trong (SAB) kẻ \(AD \bot SB\) tại D.
\(\left. \begin{array}{l}BC \bot AD\\SB \bot AD\\BC \cap SB = \left\{ B \right\}\end{array} \right\} \Rightarrow AD \bot \left( {SBC} \right) \Rightarrow \)D là hình chiếu của A trên (SBC).
b) A là hình chiếu của S trên (ABC) \(\left( {SA \bot \left( {ABC} \right)} \right)\)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABC)
\( \Rightarrow \) \(\left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {SCA} = \arctan \frac{1}{{\sqrt 2 }}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = \arctan \frac{1}{{\sqrt 2 }}\)

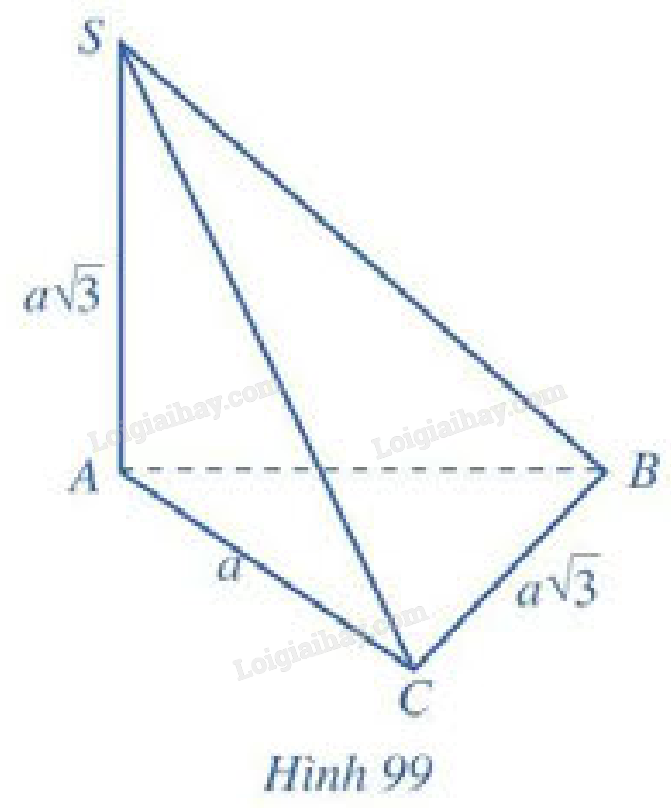
a) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC \Rightarrow \left( {SA,BC} \right) = {90^ \circ }\).
b) \(SA \bot \left( {ABC} \right) \Rightarrow \left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SCA} = {60^ \circ }\)
Vậy \(\left( {SC,\left( {ABC} \right)} \right) = {60^ \circ }\).
c) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB,SA \bot AC\)
Vậy \(\widehat {BAC}\) là góc nhị diện \(\left[ {B,SA,C} \right]\).
\(\Delta ABC\) vuông tại \(C \Rightarrow \tan \widehat {BAC} = \frac{{BC}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {BAC} = {60^ \circ }\).
d)
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AC \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAC} \right)\\ \Rightarrow d\left( {B,\left( {SAC} \right)} \right) = BC = a\sqrt 3 \end{array}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC,AC \bot BC\)
\( \Rightarrow d\left( {SA,BC} \right) = AC = a\)
g) \({S_{\Delta ABC}} = \frac{1}{2}AC.BC = \frac{1}{2}a.a\sqrt 3 = \frac{{{a^2}\sqrt 3 }}{2}\)
\(\begin{array}{l}h = SA = a\sqrt 3 \\ \Rightarrow {V_{S.ABC}} = \frac{1}{3}.{S_{\Delta ABC}}.SA = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{2}.a\sqrt 3 = \frac{{{a^3}}}{2}\end{array}\)

a) \(SA \bot \left( {ABC} \right);SA \subset \left( {SAB} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right)\)
\(\left. \begin{array}{l}AH \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AH \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAH} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAH} \right) \bot \left( {SBC} \right)\)
b) Ta có \(AH \bot BC,BC \bot SH\left( {BC \bot \left( {SAH} \right)} \right)\)
\( \Rightarrow \left[ {S,BC,A} \right] = \left( {SH,AH} \right) = \widehat {SHA}\)
Xét tam giác ABC vuông tại A có
\(\widehat {ABC} = {30^0} \Rightarrow \widehat {ACH} = {60^0}\)
Xét tam giác ACH vuông tại H có
\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} \Rightarrow AH = a.\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác SHA vuông tại A có
\(\tan \widehat {SHA} = \frac{{SA}}{{AH}} = \frac{{a\sqrt 3 }}{2}:\frac{{a\sqrt 3 }}{2} = 1 \Rightarrow \widehat {SHA} = {45^0}\)
Vậy \(\left[ {S,BC,A} \right] = {45^0}\)