Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
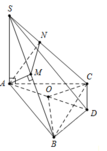
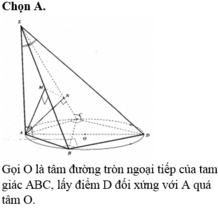
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Và D là điểm đối xứng với A qua O.


Đáp án D
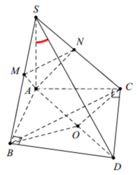
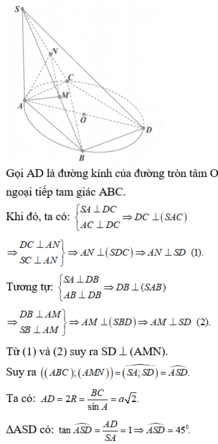
Gọi O là tâm đường tròn ngoại tiếp Δ A B C , D là điểm đối xứng với A qua O.
⇒ O A = O B = O D suy ra tam giác ABD vuồn tại B ⇒ A B ⊥ B D .
Ta có A B ⊥ B D S A ⊥ B D ⇒ B D ⊥ S A B ⇒ B D ⊥ A M suy ra A M ⊥ S B D .
Suy ra A M ⊥ S D . Tương tự, ta chứng minh được A N ⊥ S D
Do đó S D ⊥ A M N . suy ra A B C ; A M N ^ = S A ; S D ^ = A S D ^
Tam giác SAD vuông tại A, có tan A S D ^ = A D S A
Mà đường kính A D = 2 x R Δ A B C = B C sin 120 ∘ = 3 2 x S A
Vậy tan A S D ^ = 3 3 ⇒ A S D ^ = 30 ∘ ⇒ A B C ; A M N ^ = 30 ∘

Chọn B.
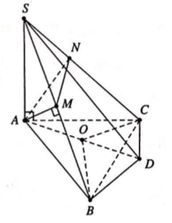
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, và D là điểm đối xứng với A qua O.
Ta có BD ⊥ AB (góc nội tiếp chắn nửa đường tròn).
Và BD ⊥ SA ⇒ BD ⊥ ( SAB ) ⇒ BD ⊥ AM .
Mặt khác AM ⊥ SB ⇒ AM ⊥ ( SBD ) ⇒ SD ⊥ AM .
Chứng minh tương tự ta được SD ⊥ AN ⇒ SD ⊥ ( AMN ) .
Ta có SD ⊥ ( AMN ) SA ⊥ ( ABC ) ⇒ ( ( AMN ) ; ( ABC ) ^ )
= ( SA ; SD ^ ) = ASD ^ .
Ta có: AD = 2 R ABC = BC sin A ^ = a 2
Vậy ( ( AMN ) ; ( ABC ) ^ ) = ASD ^ = arctan 1 = 45 o

Đáp án D
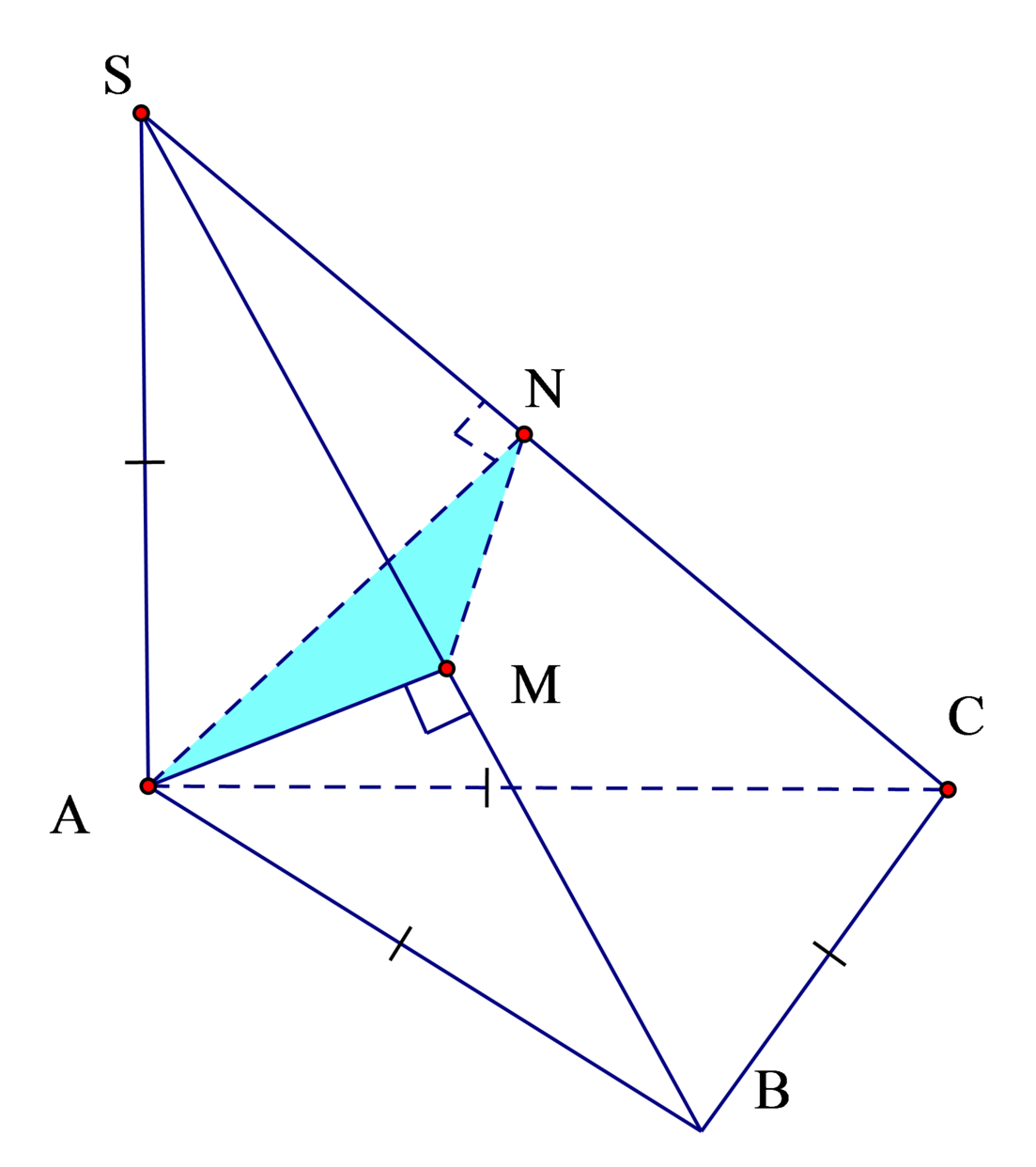
Do Δ S A B , Δ S A C cân nên M, N là trung điểm SB, SC
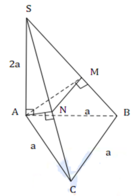
Ta có: V S . A M N V S . A B C = S M S B S N S C = 1 2 1 2 = 1 4 ⇒ V A . B C M N V S . A B C = 3 4
⇒ V A . B C M N = 3 4 V S . A B C = 1 4 S A . d t A B C = 1 4 a . a 2 3 4 = a 3 3 16


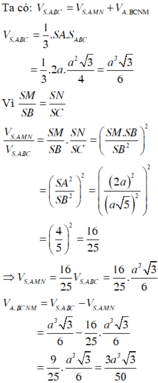

Đáp án D
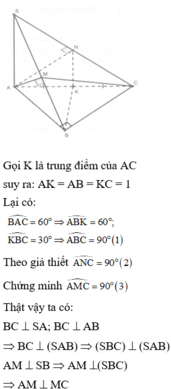
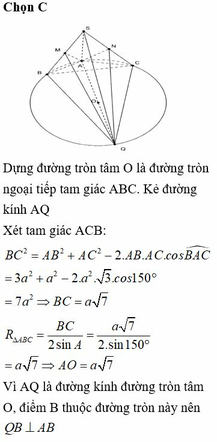
Kí hiệu như hình vẽ với D B ⊥ A B , D C ⊥ A C .
Ta có D B ⊥ S A D B ⊥ A B ⇒ D B ⊥ S B D ⇒ A M ⊥ S D .
Tương tự A N ⊥ S D ⇒ S D ⊥ A M N .
Mà S A ⊥ A B C ⇒ A B C ; A M N ^ = D S A ^ .
Ta có sin B A C ^ = B C 2 R = B C A D = 3 2 ⇒ A D = 2 B C 3 = S A 3 ⇒ tan D S A ^ = A D S A = 1 3 ⇒ D S A ^ = 30 ° .