Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Trên cạnh SB, SC lần lượt lấy các điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2 , MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong
∆
SIM, 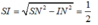
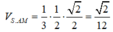
Ta có 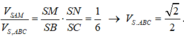

Chọn D.
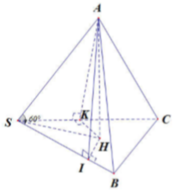
Gọi là hình chiếu vuông góc của A lên mp (SBC) . Gọi I, K lần lượt là hình chiếu vuông góc của H lên SB và SC.
Ta có 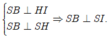
Chứng minh tương tự ta được SC ⊥ SK
∆ SAI = ∆ SAK (cạnh huyền – góc nhọn) => SI = SK
Khi đó ∆ SHI = ∆ SHK (cạnh huyền – cạnh góc vuông) => HI = HK. Do đó SH là đường phan giác trong của BSC, nên HSI = 30 °
Trong tam giác vuông SAI, ![]()
Trong tam giác vuông HIS, ![]()
![]()
Khi đó 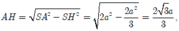
![]()
Vậy 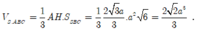
Cách 2: Sử dụng công thức tính nhanh
Nếu khối chóp S.ABC có 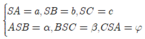 thì
thì
![]()
![]()
Áp dụng: Với ![]()
![]()
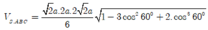
![]() Cách 3:
Cách 3:
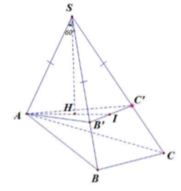
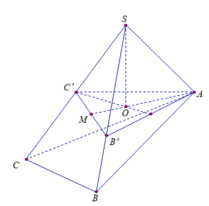
Trên các cạnh SB, SC lần lượt lấy các điểm B’, C’ sao cho SB' = SC' = SA = a 2
Khi đó chóp S.AB'C' là khối chóp tam giác đều. Đồng thời ASB = BSC = CSA = 60 ° nên AB' = B'C' = AC' = SA = a 2
Gọi H là hình chiếu của S lên mặt phẳng (AB'C'). Khi đó dễ dàng chứng minh được các tam giác SHA, SHB', SHC' bằng nhau. Suy ra HA, HB', HC' bằng nhau. Hay H là tâm đường tròn ngoại tiếp tam giác AB'C'. Vì tam giác AB'C' đều nên H cũng là trọng tâm tam giác AB'C'.
Ta có 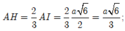
![]()
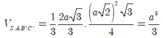
Ta có
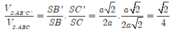
![]()

Chọn A
Gọi B' trên SB sao cho S B ' = 2 3 S B và C' trên SC sao cho S C ' = 2 3 S C .
Khi đó SA=SB'=SC'=2 => S. AB'C' là khối tứ diện đều.
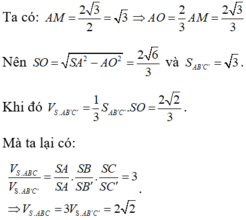
Cách khác:
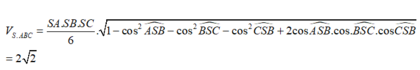

Chọn B
Lấy M ∈ S B , N ∈ S C thỏa mãn SM=SN=SA=a ⇒ S M S B = 1 2 S N S C = 1 4
Theo giả thiết: A S B ^ = B S C ^ = C S A ^ = 60 o ⇒ S . A M N là khối tứ diện đều cạnh a.
Do đó: V S . A M N = a 3 2 12
Mặt khác:
V S . A M N V S . A B C = S M S B . S N S C = 1 2 . 1 4 = 1 8 ⇒ V S . A B C = 8 V S . A M N = 2 a 3 2 3

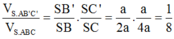
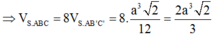

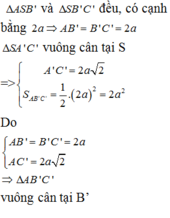

Tứ diện (hay chóp tam giác) khi biết \(SA=x;SB=y;SC=z\) và các góc tương ứng ở đỉnh: \(\widehat{ASB}=a;\widehat{BSC}=b;\widehat{CSA}=c\) sẽ có thể tích được tính bởi:
\(V=\frac{xyz}{6}\sqrt{1+2cosa.cosb.cosc-cos^2a-cos^2b-cos^2c}\)
Cụ thể trong bài này thì:
\(V=\frac{a.2a.3a}{6}.\sqrt{1+2cos\left(60\right).cos\left(90\right).cos\left(120\right)-cos^250-cos^290-cos^2120}=...\)