Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A E M B C H N S
Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

S A M I C G B H
Vì tam giác ABC vuông cân tại C, \(AB=3a\Rightarrow CA=CB=\frac{3a}{\sqrt{2}}\)
Gọi M là trung điểm \(AC\Rightarrow MC=\frac{3a}{2\sqrt{2}}\Rightarrow MB=\frac{3a\sqrt{5}}{2\sqrt{2}}\)
\(\Rightarrow BG=\frac{2}{3}BM=\frac{a\sqrt{5}}{\sqrt{2}}\Rightarrow SG=\sqrt{SB^2-BG^2}=a\)
\(\Rightarrow V_{S.ABC}=\frac{1}{3}SG.S_{\Delta ABC}=\frac{3a^2}{4}=\frac{3a^2}{4}\)
Kẻ \(GI\perp AC\left(I\in AC\right)\Rightarrow AC\perp\left(SGI\right)\)
Ta có : \(GI=\frac{1}{3}BC=\frac{a}{\sqrt{2}}\)
Kẻ \(GH\perp SI\left(H\in SI\right)\Rightarrow GH\perp\left(SAC\right)\Rightarrow d\left(G,\left(SAC\right)\right)=GH\)
Ta có \(\frac{1}{GH^2}=\frac{1}{GS^2}+\frac{1}{GI^2}\Rightarrow GH=\frac{a}{\sqrt{3}}\Rightarrow3d\left(B,\left(SAC\right)\right)=3GH=a\sqrt{3}\)

A B C D H K S
Hạ \(SH\perp BC\Rightarrow\left(SBC\right)\perp\left(ABC\right)\)
\(\Rightarrow SH\perp BC;SH=SB.\sin\widehat{SBC}=a\sqrt{3}\)
Diện tích : \(S_{ABC}=\frac{12}{\boxtimes}BA.BC=6a^2\)
Thể tích : \(V_{s.ABC}=\frac{1}{3}S_{ABC}.SH=2a^3\sqrt{3}\)
Hạ \(HD\perp AC\left(D\in AC\right),HK\perp SD\left(K\in SD\right)\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H,\left(SAC\right)\right)\)
\(BH=SB.\cos\widehat{SBC}=3a\Rightarrow BC=4HC\)
\(\Rightarrow d\left(B,\left(SAC\right)\right)=4d\left(H,SAC\right)\)
Ta có : \(AC=\sqrt{BA^2+BC^2}=5a;HC=BC-BH=a\)
\(\Rightarrow HD=BA.\frac{HC}{AC}=\frac{3a}{5}\)
\(HK=\frac{SH.HS}{\sqrt{SH^2+HD^2}}=\frac{3a\sqrt{7}}{14}\)
Vậy \(d\left(B,\left(SAC\right)\right)=4HK=\frac{6a\sqrt{7}}{7}\)

B A C H I S
Gọi H là trung điểm của BC, suy ra \(SH\perp BC\). Mà (SBC) vuông góc với (ABC) theo giao tuyến BC, nên \(SH\perp\left(ABC\right)\)
Ta có : \(BC=a\Rightarrow SH=\frac{a\sqrt{3}}{2}\); \(AC=BC\sin30^0=\frac{a}{2}\)
\(AB=BC.\cos30^0=\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABC}=\frac{1}{6}SH.AB.AC=\frac{a^3}{16}\)
Tam giác ABC vuông tại A và H là trung điểm của BC nên \(HA=HB\). Mà \(SH\perp\left(ABC\right)\), suy ra \(SA=SB=a\). Gọi I là trung điểm của AB, suy ra \(SI\perp AB\)
Do đó \(SI=\sqrt{SB^2-\frac{AB^2}{4}}=\frac{a\sqrt{13}}{4}\)
Suy ra \(d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=\frac{6V_{S.ABC}}{SI.AB}=\frac{a\sqrt{39}}{13}\)

Đáp án D
Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:


1.
\(V=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{1}{6}.a.a.2a=\frac{a^3}{3}\)
2.
\(V=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}.2a\sqrt{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3}{2}\)
P/s: chóp này là chóp "có đáy là tam giác đều" chứ không phải "chóp tam giác đều"
Hai loại này khác xa nhau đấy, ko lộn xộn nhầm lẫn được đâu
3.
Câu này đề sai
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\Rightarrow\Delta SAC\) vuông tại A
\(\Rightarrow SC>SA\) (cạnh huyền luôn lớn hơn cạnh góc vuông)
Do đó đề cho \(SA=SC\) là vô lý
4.
\(AC=BD=\sqrt{AB^2+AD^2}=2a\)
\(\widehat{SCA}=60^0\Rightarrow SA=SC.tan60^0=2a\sqrt{3}\)
\(V=\frac{1}{3}SA.AB.AD=\frac{1}{3}.2a\sqrt{3}.a.a\sqrt{3}=2a^3\)

+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)
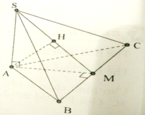
Phương pháp:
Thể tích khối chóp V = 1 3 Sh với S là diện tích đáy, h là chiều cao.
Cách giải:
Tam giác ABC đều cạnh a nên diện tích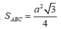
Thể tích khối chóp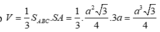
Chọn: C