

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




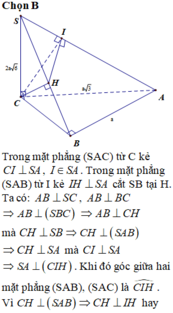
Qua C kẻ đường thẳng vuông góc AC cắt AB kéo dài tại D
\(\left\{{}\begin{matrix}SC\perp\left(ABC\right)\Rightarrow SC\perp CD\\CD\perp AC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAC\right)\)
Kẻ \(CH\perp SB\Rightarrow CH\perp\left(SAB\right)\)
\(\Rightarrow\widehat{HCD}\) là góc giữa (SAB) và (SAC)
\(BC=\sqrt{AC^2-AB^2}=a\sqrt{2}\)
\(\dfrac{1}{CH^2}=\dfrac{1}{SC^2}+\dfrac{1}{BC^2}=\dfrac{13}{24a^2}\Rightarrow CH=\dfrac{2a\sqrt{78}}{13}\)
\(CD=AC.tanA=AC.\dfrac{BC}{AB}=a\sqrt{6}\)
\(sin\widehat{HCD}=\dfrac{DH}{CD}=\dfrac{\sqrt{CD^2-CH^2}}{CD}=...\)

Chọn đáp án B
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
![]()
Ta có
![]()
Tương tự, ta cũng chứng minh được
![]()
Từ đó suy ra
![]()
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
![]()
Trong tam giác vuông ABH, ta có
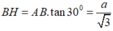
Trong tam giác vuông SHB, ta có
![]()
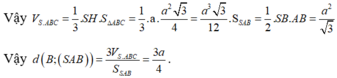

a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)