Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
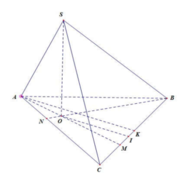
Phương pháp: Sử dụng công thức tính thể tích khối chóp khi biết ba góc ở một đỉnh và ba cạnh ở đỉnh đó.
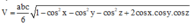
(trong đó a, b, c là độ dài ba cạnh, x, y, z là số đo ba góc ở một đỉnh)
Sau đó tính khoảng cách dựa vào công thức tính thể tích h = 3 V h .
Cách giải: Áp dụng công thức trên ta có:
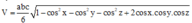
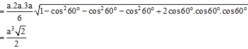


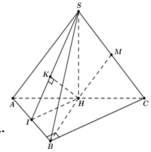
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

Đáp án D
Phương pháp:
+ Tìm tâm và bán kính của mặt cầu
+ Xác định vị trí tương đối của mặt phẳng và mặt cầu để suy ra vị trí của điểm M
+ Tìm tọa độ của đường thẳng và mặt cầu thì ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt cầu
Cách giải:
Mặt cầu (S) có tâm
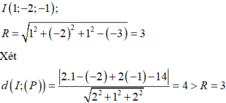
nên mặt phẳng (P) không cắt mặt cầu (S).Khi đó điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất thì M là giao điểm của đường thẳng d đi qua I , nhận n P → = 2 ; - 1 ; 2 làm VTCP với mặt cầu.
Phương trình đường thẳng
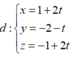
Tọa độ giao điểm của đường thẳng d và mặt cầu (S) thỏa mãn hệ phương trình
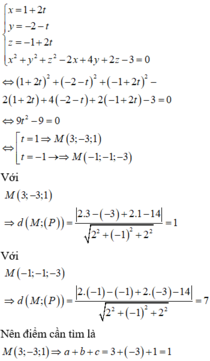

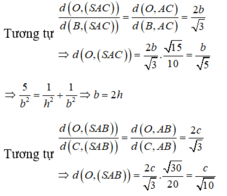
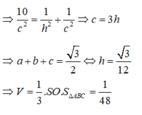


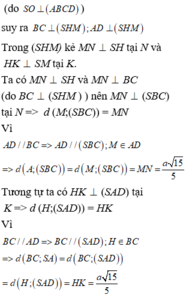




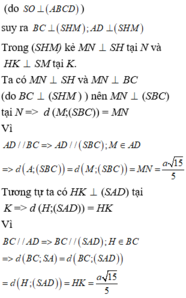



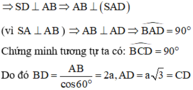

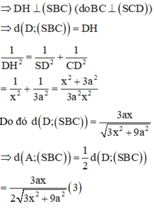


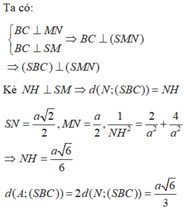
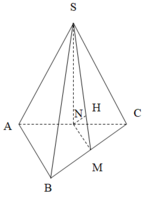
Chọn C