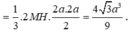Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

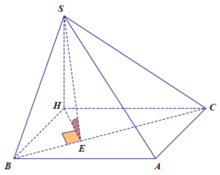
Kẻ SH vuông góc với BC tại H => SH vuông góc với (ABC)
Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
Ta có góc SMH = góc SNH = 60 độ
Dễ thấy tam giác SHM = tam giác SHN => HM = HN
Ta có HM = HB.sin 30 = 1/2 HB hay HB = 2 HM
HN = HC.sin 60 = HC.căn 3 /2 => HC = 2/căn 3.HN = 2/căn 3 .HM
=> BC = a = HB + HC = ( 2 + 2/căn 3).HM
=> HM = a/(2 + 2/căn 3) = a.căn 3 /(2+ 2.căn 3)
=> SH = HM.tan 60 = 3a/(2+2.căn 3)
Có AB = BC/2 = a/2
AC = BC.căn 3/2 = a.căn 3/2
S(ABC) = 1/2.AB.AC = 1/8.a^2.căn 3
=> V(SABC) = 1/3.3a/(2+2.căn 3) . 1/8.a^2.căn 3 = a^3.căn 3 /[16.(1+ căn 3)]

B A C H I S
Gọi H là trung điểm của BC, suy ra \(SH\perp BC\). Mà (SBC) vuông góc với (ABC) theo giao tuyến BC, nên \(SH\perp\left(ABC\right)\)
Ta có : \(BC=a\Rightarrow SH=\frac{a\sqrt{3}}{2}\); \(AC=BC\sin30^0=\frac{a}{2}\)
\(AB=BC.\cos30^0=\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABC}=\frac{1}{6}SH.AB.AC=\frac{a^3}{16}\)
Tam giác ABC vuông tại A và H là trung điểm của BC nên \(HA=HB\). Mà \(SH\perp\left(ABC\right)\), suy ra \(SA=SB=a\). Gọi I là trung điểm của AB, suy ra \(SI\perp AB\)
Do đó \(SI=\sqrt{SB^2-\frac{AB^2}{4}}=\frac{a\sqrt{13}}{4}\)
Suy ra \(d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=\frac{6V_{S.ABC}}{SI.AB}=\frac{a\sqrt{39}}{13}\)

A N B C H K S
Theo giả thiết, \(HA=HC=\frac{1}{2}AC=a\) và \(SH\perp\left(ABC\right)\)
Xét \(\Delta v.ABC\) ta có : \(BC=AC.\cos\widehat{ACB}=2a\cos30^0=\sqrt{3}a\)
Do đó : \(S_{\Delta.ABC}=\frac{1}{2}AC.BC.\sin\widehat{ACB}=\frac{1}{2}.2a.\sqrt{3}a.\sin30^0=\frac{\sqrt{3}a^2}{2}\)
Vậy \(V_{S.ABC}=\frac{1}{3}SH.S_{ABC}=\frac{1}{3}.\sqrt{2}a.\frac{\sqrt{3}}{2}a^2=\frac{\sqrt{6}a^3}{6}\)
Vì CA=2HA nên d(C,(SAB))=2d(H, (SAB)) (1)
Gọi N là trung điểm của Ab, ta có HN là đường trung bình của tam giác ABC
Do đó HN//BC suy ra AB vuông góc với HN.
Lại có AB vuông góc với Sh nên AB vuông góc với mặt phẳng (SHN).
Do đó mặt phẳng (SAB) vuông góc với mặt phẳng (SHN).
Mà Sn là giao tuyến của 2 mặt phẳng vừa nêu, nên trong mặt phẳng (SHN), hạ HK vuông góc với SN, ta có HK vuông góc với mặt phẳng (SAB)
Vì vậy d(J, (SAB)) = HK. Kết hợp với (1), suy ra d(C. (SAB))=2HK (2)
Vì \(SH\perp\left(ABC\right)\) nên \(SH\perp HN\), xét tam giác v.SHN, ta có :
\(\frac{1}{HK^2}=\frac{1}{SH^2}+\frac{1}{HN^2}=\frac{1}{2a^2}+\frac{1}{HN^2}\)
Vì HN là đường trung bình của tam giác ABC nên \(HN=\frac{1}{2}BC=\frac{\sqrt{3}a}{2}\)
Do \(\frac{1}{HK^2}=\frac{1}{2a^2}+\frac{4}{3a^2}=\frac{11}{6a^2}\) suy ra \(HK=\frac{\sqrt{66}a}{11}\) (3)
Thế (3) vào (2) ta được \(d\left(C,\left(SAB\right)\right)=\frac{\sqrt{66}a}{11}\)

Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC) \(\Rightarrow SA\perp\left(ABC\right)\)
\(AB\perp BC\Rightarrow SB\perp BC\Rightarrow\widehat{SBA}\) là góc giữa 2 mặt phẳng (SBC) và mặt phẳng (ABC)
\(\Rightarrow\widehat{SBA}=60^o\)
\(\Rightarrow SA=AB.\tan\widehat{SBA}=2a\sqrt{3}\)
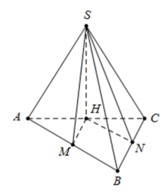
Mặt phẳng qua SM và song song với BC, cắt AC tại N
\(\Rightarrow MN||BC\) và N là trung điểm của \(AC\\ \)
\(MN=\frac{BC}{2}=a;BM=\frac{AB}{2}=a\)
Diện tích \(S_{BCNM}=\frac{\left(BC+MN\right).BM}{2}=\frac{3a^2}{2}\)
Thể tích \(V_{S.BCNM}=\frac{1}{3}S_{BCNM}.SA=a^3\sqrt{3}\)
Kẻ đường thẳng \(\Delta\) đi qua N, song song với AB
Hạ \(AD\perp\Delta\left(D\in\Delta\right)\Rightarrow AB||\left(SND\right)\)
\(\Rightarrow d\left(AB;SN\right)=d\left(AB,\left(SND\right)\right)=d\left(A,\left(SND\right)\right)\)
Hạ \(AH\perp SD\left(H\in SD\right)\Rightarrow AH\perp\left(SND\right)\Rightarrow d\left(A,\left(SND\right)\right)=AH\)
Tam giác SAD vuông tại A : \(\begin{cases}AH\perp SD\\AD=MN=a\end{cases}\)
\(\Rightarrow d\left(AB,SN\right)=AH=\frac{SA.AD}{\sqrt{SA^2+AD^2}}=\frac{2a\sqrt{39}}{13}\)

Đáp án là B
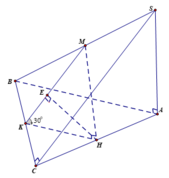
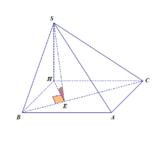
Gọi H, K, M lần lượt là trung điểm của AC, BC, SB và vì tam giác ABC vuông tại B suy ra HK ⊥ BC (1)
Gọi E là hình chiếu của H trên mặt phẳng (SBC) => HE ⊥ BC(2).
Từ (1), (2) suy ra EK ⊥ BC => EK ≡ MK( vì MK ⊥ BC) do đó
![]()
![]()
Lại có HA = HB = HC, MA = MB = MC ( do M là tâm mặt cầu ngoại tiếp S.ABC) suy ra MH là trục của đường tròn ngoại tiếp tam giác ABC suy ra ∆ MHK vuông tại H => MH = tan30 ° . H K = a 3 .
Vậy thể tích khối chóp
![]()