Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
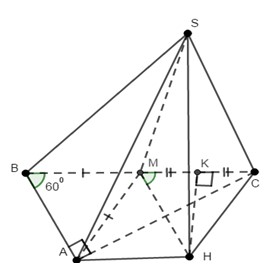
Tam giác ABM có A M = B M A B C ⏜ = 60 ° ⇒ Δ A B M đều cạnh a
Gọi H là tâm đường tròn ngoại tiếp Δ A B M
Mà S A = S B = S M ⇒ H là hình chiếu của S trên m p A B M
Tam giác SAH vuông tại H, có A H = a 3 3 ; S A = a 39 3
Suy ra S H = S A 2 − A H 2 = a 39 3 2 − a 3 3 2 = 2 a
Vậy d S ; ( A B C = S H = 2 a

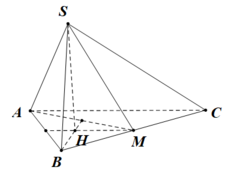
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

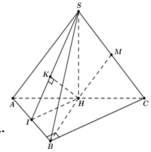
Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
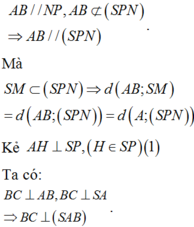
Mà
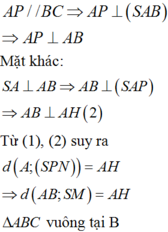
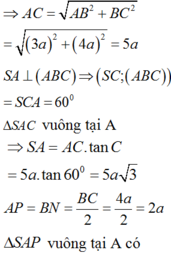
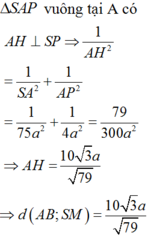
Chọn: B

Đáp án A

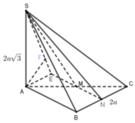
Do S A ⊥ A B C nên góc giữ SC và A B C là góc S C A ^ = 60 °
Vì Δ A B C vuông tại B nên A C = 5 a ⇒ S A = 5 a 3
Gọi N là trung điểm BC nên M N / / A B ⇒ A B / / S M N
d A B , S M = d A B , S M N = d A , S M N .
Từ A kẻ đường thẳng song song vơi BC cắt MN tại D.
Do B C ⊥ A B ⇒ B C ⊥ M N ⇒ A D ⊥ M N .
Từ A kẻ AH vuông góc vơi SD
Ta có M D ⊥ A D M D ⊥ S A ⇒ M D ⊥ S A D ⇒ M D ⊥ A H
Mà A H ⊥ S D ⇒ A H ⊥ S M D hay A H ⊥ s m n ⇒ d A , S M N = A H
Do A D = B N = 1 2 B C = 2 a .
Xét Δ S A D có 1 A H 2 = 1 S A 2 + 1 A D 2 = 1 75 a 2 + 1 4 a 2 = 79 300 a 2
⇒ d A B , S M = A H = 10 237 a 79 = 10 3 a 79

Chọn đáp án A
Phương pháp
Sử dụng lý thuyết: Góc giữa hai đường thẳng chéo nhau a, b bằng góc giữa đường thẳng a với mặt phẳng (P) chứa b mà song song với a.
Cách giải
Gọi N là trung điểm của BC thì AB//MN suy ra d(AB,SM)=d(AB,(SMN))=d(A,(SMN))
Gọi E là hình chiếu của A lên MN
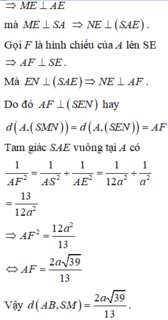

Đáp án D
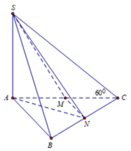
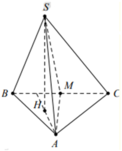
Gọi N là trung điểm của BC
Ta có A B / / M N ⇒ d A B ; S M = d A ; S M N
S A = A C tan 60 ° = 5 a 3
S M = 5 a 3 2 + 5 a 2 2 = 5 a 13 2
S N 2 = S B 2 + B N 2 = S A 2 + A B 2 + B C 2 2 = 5 a 3 2 + 3 a 2 + 2 a 2 = 88 a 2
⇒ S N = 2 a 22
M N = A B 2 = 3 a 2
Ta có:
S M 2 = N S 2 + N M 2 − 2 N S . N M . c o s M N S ^ ⇔ 5 a 13 2 22 = 88 a 2 + 3 a 2 2 − 2.2 a . 22 . 3 a 2 c o s M N S ^
c o s M N S ^ = 3 2 22 ⇒ sin M N S ^ = 79 88
S S M N = 1 2 N M . N S . s i n M N S ⏜ = 1 2 . 3 a 2 .2 a 22 . 79 88 = 3 a 2 79 4
S A M N = 1 4 S A B C = 1 4 . 1 2 .3 a .4 a = 3 a 2 2 ; V S . A M N = 1 3 S A . S A M N = 1 3 .5 a 3 . 3 a 2 2 = 5 a 3 3 2
d A ; S M N = 3 V S . A M N S S M N = 3. 5 a 3 3 2 3 a 2 79 4 = 10 a 3 79