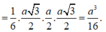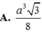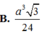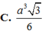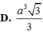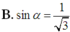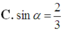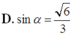Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
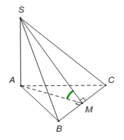
Gọi M là trung điểm của BC, suy ra AM ⊥ BC.
Ta có
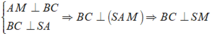
Do đó
![]()
Tam giác ABC đều cạnh a, suy ra trung tuyến AM = a 3 2
Tam giác vuông SAM, có
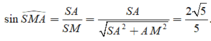

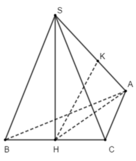
+ Gọi H là trung điểm của BC
Do tam giác ABC cân tại A nên AH ⊥ BC, tam giác SBC đều nên SH ⊥ BC
Mà (SBC) ⊥ (ABC)
Do đó SH ⊥ (ABC)
+ Gọi K là hình chiếu vuông góc của H lên SA ⇒ HK ⊥ SA
Ta có B C ⊥ S H B C ⊥ A H ⇒ B C ⊥ S A H ⇒ B C ⊥ H K
Vậy HK là đoạn vuông góc chung của BC và SA, do đó khoảng cách giữa BC và SA là HK.
+ Tính HK
Tam giác SBC đều cạnh a ⇒ SH = a 3 2
Tam giác ABC vuông cân tại A ⇒ AH = B C 2 = a 2
Tam giác SHA vuông tại H có HK là đường cao ⇒ 1 H K 2 = 1 S H 2 + 1 A H 2
HK = a 3 4
Vậy d(SA; BC) = a 3 4 .
Đáp án C

Chọn A
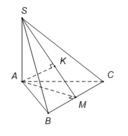
Gọi M là trung điểm BC
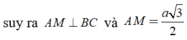
Gọi K là hình chiếu của A trên SM , suy ra AK ⊥ SM. (1)
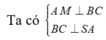
![]()
![]()
![]()
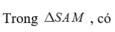
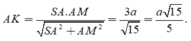
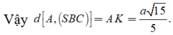

Đáp án B
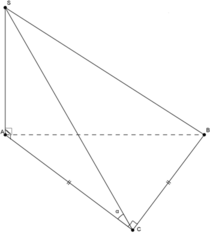
Ta có BC ⊥ AC và BC ⊥ SC, do đó góc giữa mp (SBC) và mp (ABC) chính là góc SCA.
Mặt khác
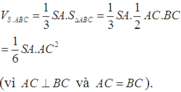
Vì tam giác SAC vuông tại A nên ta có
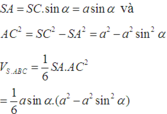
đặt t = sin α ta có hàm số thể tích theo t như sau
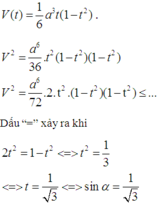

Đáp án D.
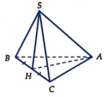
Gọi H là trung điểm của BC ![]()
∆ SBC đều cạnh bằng a nên
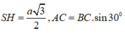
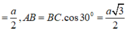
![]()