Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

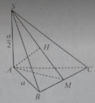
\(\Delta ABC\) đều \(\Rightarrow AM\perp BC\) (1)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAM\right)\)
b/ \(BC\perp\left(SAM\right)\) mà BC là giao tuyến của (SBC) và (ABC)
\(\Rightarrow\widehat{SMA}\) là góc giữa (SBC) và (ABC)
\(AM=\frac{AB\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\Rightarrow tan\widehat{SMA}=\frac{SA}{AM}=2\)
\(\Rightarrow\widehat{SMA}\approx63^026'\)
c/ Từ A kẻ \(AH\perp SM\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\frac{1}{AH^2}=\frac{1}{AM^2}+\frac{1}{SA^2}\Rightarrow AH=\frac{AM.SA}{\sqrt{AM^2+SA^2}}=\frac{a\sqrt{15}}{5}\)

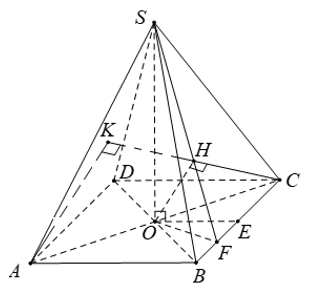
a có \(\angle \left(\right. S C , \left(\right. A B C D \left.\right) \left.\right) = 45^{\circ}\).
Nghĩa là hình chiếu của \(S\) xuống đáy nằm trên đường chéo \(B D\).
Xét tam giác cân \(S A B\), do tính đối xứng ⇒ khoảng cách từ \(A\) đến \(\left(\right. S C D \left.\right)\) chính bằng nửa cạnh hình vuông:
\(d\left(\right.A,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{2}\)
Với \(M\) là trung điểm \(S A\), khoảng cách giảm đi một nửa:
\(d\left(\right.M,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{4}\)
Đáp số
\(d \left(\right. A , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{2}\)
\(d \left(\right. M , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{4}\)






tam giác ABC đều nên AM ⊥ BC ⇒ SM ⊥ BC (theo định lí ba đường vuông góc)
Đáp án B