Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8:
Kẻ \(AH\perp SM\)
Trong mặt phẳng (SBC), qua H kẻ đường thẳng song song BC cắt SB và SC lần lượt tại P và Q
\(\Rightarrow\Delta APQ\) là thiết diện của (P) và chóp
\(AM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow SA=AM\Rightarrow\Delta SAM\) vuông cân tại A
\(\Rightarrow AH=\frac{SA\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\) đồng thời H là trung điểm SM
\(\Rightarrow PQ=\frac{1}{2}BC=\frac{a}{2}\) (đường trung bình)
\(\Rightarrow S_{\Delta APQ}=\frac{1}{2}AH.PQ=\frac{a^2\sqrt{6}}{16}\)
Câu 9.
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=AH=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAH\) vuông cân tại H
\(\Rightarrow\widehat{SAH}=45^0\)
Câu 6:
Bạn kiểm tra lại đề, \(SO\perp\left(ABCD\right)\Rightarrow SO\perp OB\Rightarrow\widehat{SOB}=90^0\)
Nên không thể có chuyện \(tan\widehat{SOB}=\frac{1}{2}\)
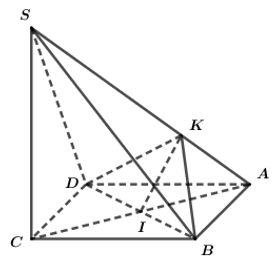
Câu 7:
H là trực tâm tam giác ABC \(\Rightarrow BH\perp AC\)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
K là trực tâm tam giác SBC \(\Rightarrow BK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BHK\right)\Rightarrow\) góc giữa SC và (BHK) bằng 90 độ






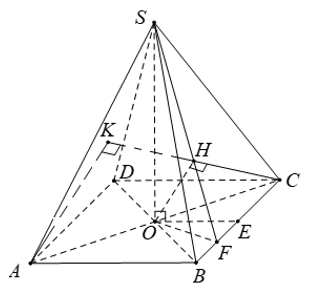


Đáp án D
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
Vậy