Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Hướng dẫn giải:
Ta có S A B C = a 2 2 , S A = S B 2 - A B 2 = a 3
V S . A B C = 1 3 S A . S A B C = 1 3 a 3 . a 2 2 = a 3 3 6
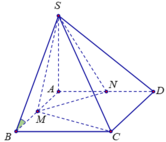
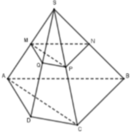
Ta lại có V B . N A M V B . C A S = B N B C . B M B S = 1 4
⇒ V B . N A M = 1 4 V B . C A S
Kết luận V A . S C N M = V S . A B C - V B . N A M = a 3 3 8

Chọn C
![]()
![]()
nên góc giữa mặt phẳng (SBC) và (ABCD) là . Do đó SA = AB tan450 = a
Mặt khác:
![]()
Vậy:
![]()

Theo công thức Simsons ta có:
\(\dfrac{V_{SMNPQ}}{V_{SABCD}}=\dfrac{2V_{SMNP}}{2V_{SABC}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}.\dfrac{SP}{SC}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{8}\)

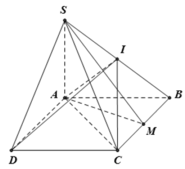
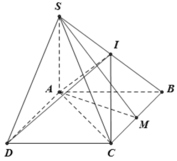
* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
![]()
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và ![]() nên ΔABC đều.
nên ΔABC đều.
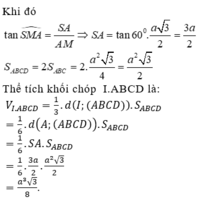
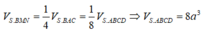
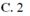



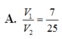


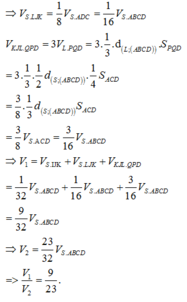
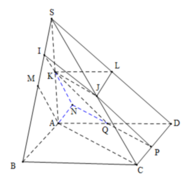
M là trung điểm SA \(\Rightarrow d\left(M;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)\)
N là trung điểm MC \(\Rightarrow d\left(N;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(M;\left(ABCD\right)\right)=\dfrac{1}{4}d\left(S;\left(ABCD\right)\right)\)
\(\Rightarrow V_{NABCD}=\dfrac{V}{4}\)