Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB=BC.cos60^0=a\) ; \(AC=BC.sin60^0=a\sqrt{3}\)
\(AH=\frac{AB.AC}{BC}=\frac{a\sqrt{3}}{2}\)
a/ Do \(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC) \(\Rightarrow\widehat{SAH}=60^0\)
\(\Rightarrow SH=AH.tan60^0=\frac{3a}{2}\)
b/ \(AC^2=HC.BC\Rightarrow HC=\frac{AB^2}{BC}=\frac{3a}{2}\)
\(EH||AB\Rightarrow\frac{EH}{AB}=\frac{HC}{BC}\Rightarrow EH=\frac{AB.HC}{BC}=\frac{3a}{4}\)
Do \(SH\perp\left(ABC\right)\Rightarrow\widehat{SEH}\) là góc giữa SE và (ABC)
\(tan\widehat{SEH}=\frac{SH}{EH}=2\)
c/ Không biết (SH3) là gì bạn?

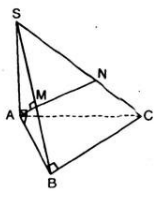
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:


\(\left\{{}\begin{matrix}BD\perp SA\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)

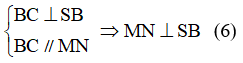



a a a I A B C S 120độ
Gọi I là trung điểm của BC
tam giác SBC đều cạnh a
=> SI \(\perp\) BC
Mà : BC \(\perp\) SA (SA \(\perp\)(ABC))
=> BC \(\perp\) (SAI) => BC \(\perp\) AI
=> \(S_{ABC}=\dfrac{1}{2}BC.AI\)
Ta có : Tam giác ABC có đường trung tuyến AI là đường cao
=> Tam giác ABC cân tại A
-> AI là phân giác
Xét \(\Delta\) vuông \(AIB\) có : \(AI=BI.cot60^o\)
= \(\dfrac{a}{2}\cdot\dfrac{1}{\sqrt{3}}=\dfrac{a}{2\sqrt{3}}\)
Xét \(\Delta\) vuông \(SAI\) có :
\(SA=\sqrt{SI^2-AI^2}\)
\(SI\) là đường cao của \(\Delta\) đều cạnh a => SI = \(\dfrac{a\sqrt{3}}{2}\)
=> SA = \(\sqrt{\dfrac{3a^2}{4}-\dfrac{a^2}{12}}=\dfrac{a\sqrt{2}}{\sqrt{3}}\)
=> \(V_{SABC}=\dfrac{1}{3}S_{ABC}.SA=\dfrac{1}{3}\cdot\dfrac{a^2}{4\sqrt{3}}\cdot\dfrac{a\sqrt{2}}{\sqrt{3}}=\dfrac{1}{3}\cdot\dfrac{a^3\sqrt{2}}{36}\)
Vậy ......
Ps : Viết sai SABC thành \(S_{ABC}\) ; SBC thành \(S_{BC}\) ;
SA \(\perp\) (ABC) thành \(S_{A\perp\left(ABC\right)}\) ; \(V_{SABC}\) thành \(V_{S_{ABC}}\) . Lần sau viết cho cẩn thận
t nhìn cái đề nó thế thì viết thế thôi