Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

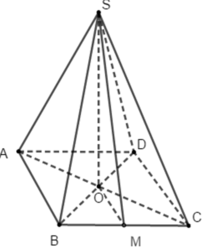
Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
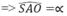
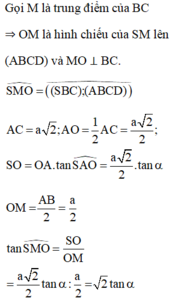
Đáp án C

Chọn D
Phương pháp
Góc giữa cạnh bên SA với mặt đáy là góc giữa SA và hình chiếu của SA trên mặt phẳng đáy.
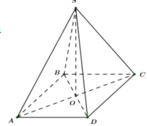
Gọi O là giao điểm của AC và BD
Ta có SABCD là hình chóp đều nên O là hình chiếu của S trên
(ABCD).
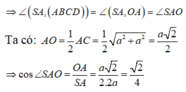

Chọn C
Xác định được
![]()
Khi đó ta tính được
![]()
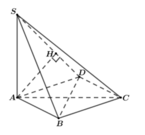
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
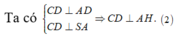
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
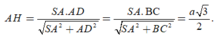
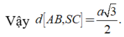

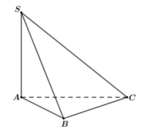
Gọi O là tâm đáy, M là trung điểm AB
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy
\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)
\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)

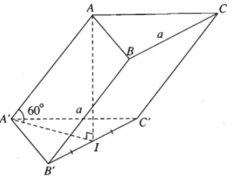
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
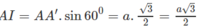
b) 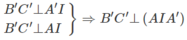
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

Chọn đáp án B

Gọi G là trọng tâm tam giác đều ABC, E là trung điểm của SA, K, H là hình chiếu của G, E lên SA.
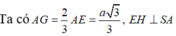
HE ⊥ BC vì HE là trung tuyến trong tam giác cân HBC.
Suy ra HE là đoạn vuông góc chung của SA và BC
![]()
Xét tam giác SAG vuông tại G. SG = tan 60 0 .AG = a
![]()



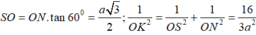
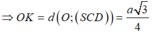
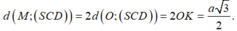
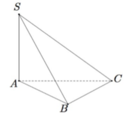

Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.
Gọi AG cắt BC tại D
a) Ta có A là hình chiếu của A trên (ABC)
G là hình chiếu của S trên (ABC)
\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)
\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác SAG vuông tại G có
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)
b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(BC \bot AD\) (G là trực tâm)
\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)
Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)
Xét tam giác SGD vuông tại G có
\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)