Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

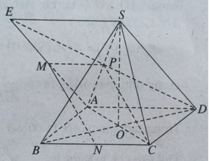
Gọi P là trung điểm SA, ta có MPCN là hình bình hành.
Như vậy MN // PC, suy ra MN // (SAC).
Do BD ⊥ (SAC) nên BD ⊥ MN.
Ta có: d(MN, AC) = d(N, (SAC))
Mà C ∈(SAC) & CN/CB = 1/2
Nên d(N, (SAC)) = 1/2 d(B, (SAC)) = 1/2 BO (O là giao điểm của AC và BD).
Vậy d(N, (SAC)) = 1/4a√2.

Câu hỏi của Phạm Thùy Dương - Toán lớp 11 - Học toán với OnlineMath
Em tham khảo bài làm tại link này nhé!
Cộng đồng học tập online | Học trực tuyến
Lần sau các bài Toán lớp 10, 11, 12 các em đăng trong trang Cộng đồng học tập online | Học trực tuyến nhé! olm hầu như để giải đáp thắc mắc của HỌc sinh tiểu học và trung học em nhé :). Chúc em học tập tốt :)<3

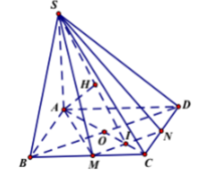
AM là hình chiếu của SM trên (ABCD).
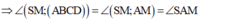
- Xét tam giác vuông ABM ta có: 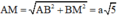
- Xét tam giác vuông SAM ta có: 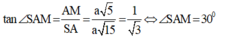

a: BD cắt AC tại E
b: Xét ΔSAC có SM/SA=SN/SC
nên MN//AC
c: Trong mp(SAC), ta có: SE không song song với MN
=>SE cắt MN tại K
d: \(C\in SN\)
\(C\in\left(ABCD\right)\)
Do đó: \(SN\cap\left(ABCD\right)=C\)

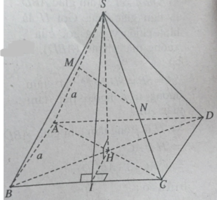
a) (AC ⊥ SH & AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD.
b) (MN//AC & AC ⊥ (SBD) ⇒ MN ⊥ (SBD).
c) + Xác định góc α giữa (SBC) và (ABCD)
Gọi I là trung điểm của BC, ta có:
(BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH)
⇒ BC ⊥ SI.
⇒ [((SBC),(ABCD)) ] = ∠(SIH) = α.
+ Tính α:
Trong tam giác SIH, ta có: cosα = IH/IS = √3/3 ⇒ α = arccos√3/3.

Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)

Đáp án C
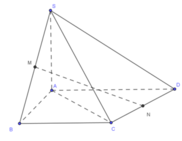
Kẻ CN
⊥
AB ta dễ dàng tính được ![]()
![]()
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
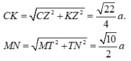
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
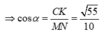

.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC
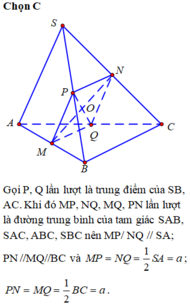

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Tứ giác SDAE là hbh (hai đường chéo cắt nhau tại trung điểm)
Gọi H là hình chiếu của E trên (ABCD)
\(\left\{{}\begin{matrix}SE=AD\\SE//AD\end{matrix}\right.\) \(\Rightarrow H\) đối xứng O qua AB
Gọi K là hình chiếu của M lên (ABCD)
\(\Rightarrow\) K là trung điểm AH
Tứ giác AOBH là hbh (2 đường chéo cắt nhau tại trung điểm)
\(\Rightarrow AH//BD\)
Gọi P là trung điểm AB \(\Rightarrow KP//OA\) (đường trung bình)
Mà \(KN//AC\) (đường trung bình)
\(\Rightarrow K;P;N\) thẳng hàng
\(KN//AC\) ; \(AC\perp BD\Rightarrow KN\perp BD\)
\(\Rightarrow BD\perp\left(KMN\right)\Rightarrow BD\perp MN\)