Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

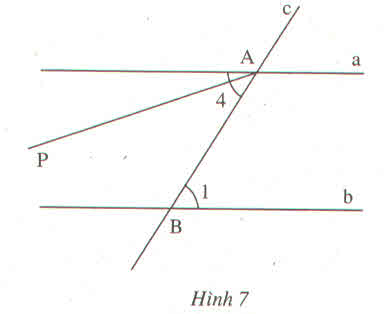
a) ˆB3B3^
b) ˆB2B2^
c) 1800 ; là cặp góc trong cùng phía
d) Bằng cặp góc so le trong ˆB2B2^=ˆA4A4^.
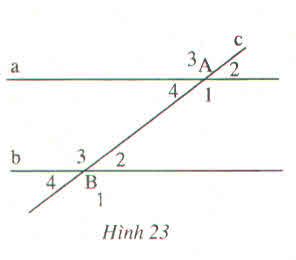
a) \(\widehat{A_1}\)\(=\widehat{B_3}\)(vì là cặp góc so le trong)
b)\(\widehat{A_2}\)\(=\widehat{B_2}\)(vì là cặp góc đồng vị)
c)\(\widehat{B_3}\)\(+\widehat{A_4}\)\(=180^0\)(vì là cặp góc trong cùng phía)
d)\(\widehat{A_2}\)\(=\widehat{B_4}\)(vì là cặp góc cùng bằng \(\widehat{A_4}\) )
Ủng hộ mk nhé!!! ^.^

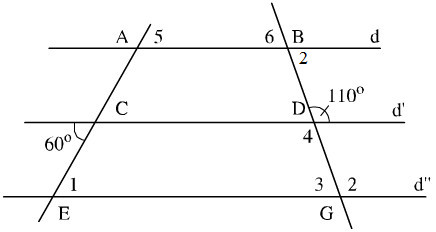
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2

a: dong vi
b: trong cung phia
c :đổng vị
d :ngoài cùng phía
e :???
g:CDE,MED
h:DBC,EBA
a)...đồng vị
b)...trong cùng phía
c)...đồng vị
d)...ngoài cùng phía
e)...so le trong
g)...MED và EDC
h)...MED và EBC
tớ thấy cậu ghi sai đề rồi tớ chỉ làm theo sách

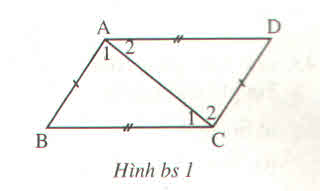
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)

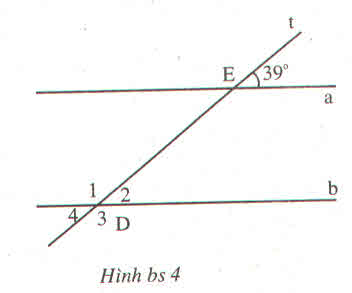
a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:
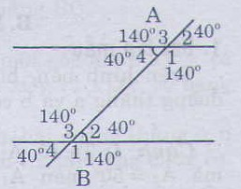
c) Ta có:
góc A4 + A1 = 180độ
=> góc A1 = 180 độ - 40 độ = 140 độ
=> góc A1 + góc B2= 40độ + 140 độ = 180 độ
Ý 2
Ta có:
góc B3 + góc B2 = 180 độ
=> góc B3 = 180 độ - 40 độ = 140 độ
=> góc A4 + B3 = 140 độ + 40 độ = 180 độ

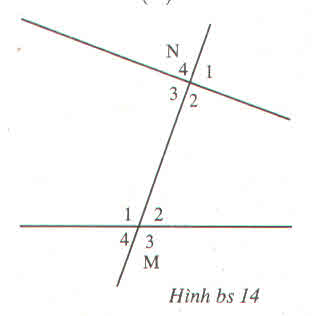
a) ˆIPOIPO^ và ˆPORPOR^ là một cặp góc so le trong..........
b) ˆOPIOPI^ và ˆTNOTNO^ là một cặp góc .....đồng vị.....
c) ˆPIOPIO^ và ˆNTONTO^ là một cặp góc ....đồng vị.....
d) ˆOPROPR^ và ˆPOIPOI^ là một .cặp góc so le trong
.........








Câu D
D