Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

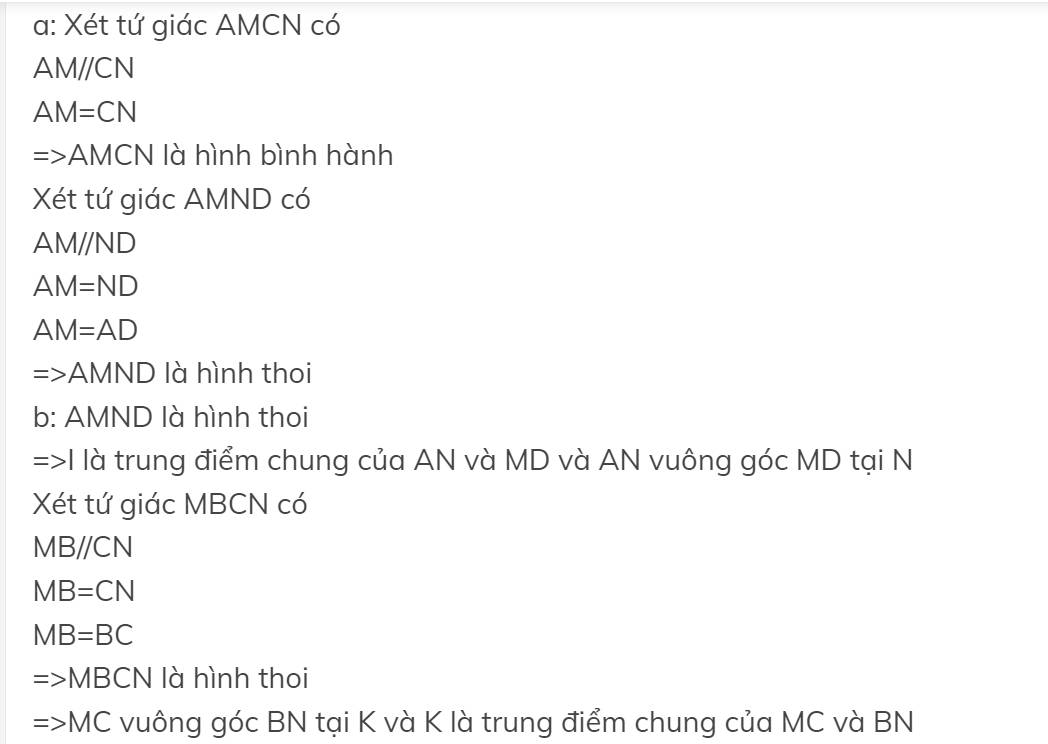
a: Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
Xét tứ giác AMND có
AM//ND
AM=ND
AM=AD
=>AMND là hình thoi
b: AMND là hình thoi
=>I là trung điểm chung của AN và MD và AN vuông góc MD tại N
Xét tứ giác MBCN có
MB//CN
MB=CN
MB=BC
=>MBCN là hình thoi
=>MC vuông góc BN tại K và K là trung điểm chung của MC và BN
Xét ΔMDC có
MN là trung tuyến
MN=DC/2
=>ΔMDC vuông tại M
Xét tứ giác MINK có
góc MIN=góc MKN=góc IMK=90 độ
=>MINK là hình chữ nhật
c: Xét ΔMDC có MI/MD=MK/MC
nên IK//DC

a) Xét tứ giác AMCN có AM // NC ( ABCD là hbh)
AM = NC (gt)
\(\Rightarrow\) AMCN là hbh (dấu hiệu nhận biết)
Xét tứ giác AMND có AM // ND ( ABCD là hình bình hành)
AM = ND (gt)
\(\Rightarrow\) AMND là hbh ( dấu hiệu nhận biết)
c) CMTT : MBCN là hbh có CM cắt BN tại K
\(\Rightarrow\) MK = KC
Hbh AMND có I là giao của AN và DM
\(\Rightarrow\) IM = ID
Xét tam giác MCD có MK = KC (cmt)
IM = ID (cmt)
\(\Rightarrow\) IK là đường trung bình của tam giác MCD ( tính chất của đường trung bình trong tam giác)
\(\Rightarrow\) IK // CD (đpcm)

File: undefined chắc các bạn cũng thấy câu a) và b) ạ. Mình làm thử có thiếu sót mong bổ xung ạ.
C) gọi giao điểm của AN và CD là O
Xét ∆ABN và ∆OCN, ta có:
NC=NB( giả thiết)
NOC = NAB ( góc so le trong)
CNO = BNA ( đối đỉnh )
=> ∆ ABN = ∆OCN ( g-c-g)
=> CO=CA ( cặp cạnh tương ứng bằng nhau)
Mà tứ giác ABCD là hình vuông
=> AB=CD=CO hoặc CD =CO
Vì ∆APM là tam giác vuông tại P
=> Gốc DPN =90°
Xét ∆ vuông DPO, ta có ( vì gốc DPN =90° cmt)
Ta có CD=CO ( cmt)
DPO =90°
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền
=> DC=PC=CO
=> ∆ DPC cân tại C ( vì CP= CD) ( đpcm)



a) Ta có: \(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(DN=NC=\dfrac{DC}{2}\)(N là trung điểm của DC)
mà AB=DC(Hai cạnh đối trong hình bình hành ABCD)
nên AM=MB=DN=NC
Xét tứ giác AMCN có
AM//CN(AB//CD, M∈AB, N∈CD)
AM=CN(cmt)
Do đó: AMCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét tứ giác AMND có
AM//ND(AB//CD, M∈AB, N∈CD)
AM=ND(cmt)
Do đó: AMND là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Ta có: \(AB=2\cdot AM\)(M là trung điểm của AB)
mà \(AB=2\cdot AD\)(gt)
nên AM=AD
Hình bình hành AMND có AM=AD(cmt)
nên AMND là hình thoi(Dấu hiệu nhận biết hình thoi)
⇒Hai đường chéo AN và DM vuông góc với nhau tại trung điểm của mỗi đường(Định lí hình thoi)
hay AN⊥DM(đpcm)
c) Ta có: AN và DM vuông góc với nhau tại trung điểm của mỗi đường(cmt)
mà AN cắt DM tại E(gt)
nên E là trung điểm chung của AN và DM
Xét tứ giác BMNC có
BM//NC(AB//CD, M∈AB, N∈CD)
BM=NC(cmt)
Do đó: BMNC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
⇒Hai đường chéo BN và MC cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà BN cắt MC tại F(gt)
nên F là trung điểm chung của MC và BN
Ta có: \(EN=\dfrac{AN}{2}\)(E là trung điểm của AN)
\(MF=\dfrac{MC}{2}\)(F là trung điểm của MC)
mà AN=MC(Hai cạnh đối trong hình bình hành AMCN)
nên EN=MF
Ta có: AN//MC(Hai cạnh đối trong hình bình hành AMCN)
mà E∈AN(cmt)
và F∈MC(cmt)
nên EN//MF
Ta có: AN⊥MD(cmt)
mà AN cắt MD tại E(gt)
nên NE⊥ME tại E
hay \(\widehat{MEN}=90^0\)
Xét tứ giác EMFN có
EN//MF(cmt)
EN=MF(cmt)
Do đó: EMFN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành EMFN có \(\widehat{MEN}=90^0\)(cmt)
nên EMFN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
⇒EF=MN(Hai đường chéo trong hình chữ nhật EMFN)
Bạn ơi bài này dễ mừ