Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
íu biết thì cut hộ
Gọi T,G là giao điểm DE,BF với AC
Ta có:AB=CD nên \(\frac{1}{2}AB=\frac{1}{2}CD\Rightarrow EB=DF\) mà \(EB//DF\) nên tứ giác EBFD là hình bình hành => ED//BF
Xét \(\Delta\)ABG có EA=EB;ET//BG nên T là trung điểm AG hay TA=TG ( 1 )
Xét \(\Delta\)CDT có FD=FC;FG//DT nên G là trung điểm CT hay TG=GC ( 2 )
Từ ( 1 ) và ( 2 ) suy ra đpcm
dễ dàng chứng minh được EBFD là hình bình hành => FB // DE
gọi I là giao điểm của DE và AC ; K là giao điểm của FB và AC
ta có: FB là đường trung bình của tam giác DIC => FB chia IC thành hai đoạn bằng nhau (1)
tương tự chứng minh được DE là đường trung bình của tam giác AKB => DE chia AK thành hai đoạn bằng nhau (2)
Từ 1 và 2 => đpcm
*Bên trên là gợi ý thôi bạn tự trình bày nhé =))))
Bạn tự vẽ hình nha ^^
a) Ta có: AB=CD (gt), mà E,F lần lượt và trung điểm của AB và CD.
=> EA=EB=FD=FC
Ta có: AB song song => EA song song FC
Ta có EA=FC và EA song song FC
=> AECF là hình bình hành.
Tương tự chứng minh BEDF là hình bình hành.
b) Kẻ EF.
Ta có: EA=FD (cmt); AB song song CD => EA song song FD
=> AEFD là hình bình hành
Tương tự chứng minh EBCF là hình hình hành.
Ta có: E là trung điểm AB
K là trung điểm của BF (hai đường chéo EC và BF của hình bình hành cắt nhau tại trung điểm mỗi đường)
=> KE là đường trung bình của tam giác ABF
=> KE song song AF và KE=1/2 AF (1)
Ta có hai đường chéo AF và DE của hình bình hành AEFD => I là trung điểm của AF => IF=1/2 AF (2)
Từ (1) và (2) suy ra IF=KE và KE song song AF
=> EIFK là hình bình hành
c) Xét hình bình hành ABCD có AC và BD là hai đường chéo => AC và BD cắt nhau tại trung điểm mỗi đường (1)
Xét hình bình hành AEFC có hai đường chéo là EF và AC => EF và AC cắt nhau tại trung điểm mỗi đường (2)
Từ (1) và (2) suy ra AC, BD, EF cùng đi qua một diểm.
d) Giả sử EIFK là hình vuông.
=> IF = IE
Mà IF=IA, IE=ID (hai đường chéo AF và DE cắt nhau tại trung điểm mỗi đường)
=> IE=ID=IA=IF
=> AF=DE
Hình bình hành AEFD có hai đường chéo bằng nhau => là hình chữ nhật.
=> DAE= 90 độ
Ta có hình bình hành ABCD có một góc vuông => là hình chữ nhật.
Vậy để EIFK là hình vuông thì ABCD phải là hình chữ nhật.
e) Gọi giao điểm của AC và DB là O
Ta có DO là đường trung tuyến xuất phát từ đỉnh D của tam giác DAC
AF là đường trung tuyến xuất phát từ đỉnh A của tam giác DAC
DO và AF cắt nhau tại M
=> M là trọng tâm của tam giác DAC
=> DM=2/3 DO, MO=1/3 DO (1)
Tương tự chứng minh NB=2/3 BO và NO=1/3 BO (2)
Ta có OB=OD (3)
Từ (1), (2) và (3) suy ra DM=NB
Ta có MN=MO+NO=1/3 DO+ 1/3 BO= 2/3 DO = 2/3 BO
=> DM=MN=NB
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Xét ΔDNC có
F là trung điểm của DC
FM//NC
Do đó: M là trung điểm của DN
Suy ra: DM=MN(1)
Xét ΔABM có
E là trung điểm của AB
EN//AM
Do đó: N là trung điểm của BM
Suy ra: BN=NM(2)
Từ (1) và (2) suy ra DM=MN=NB
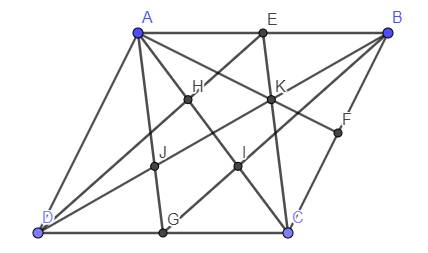
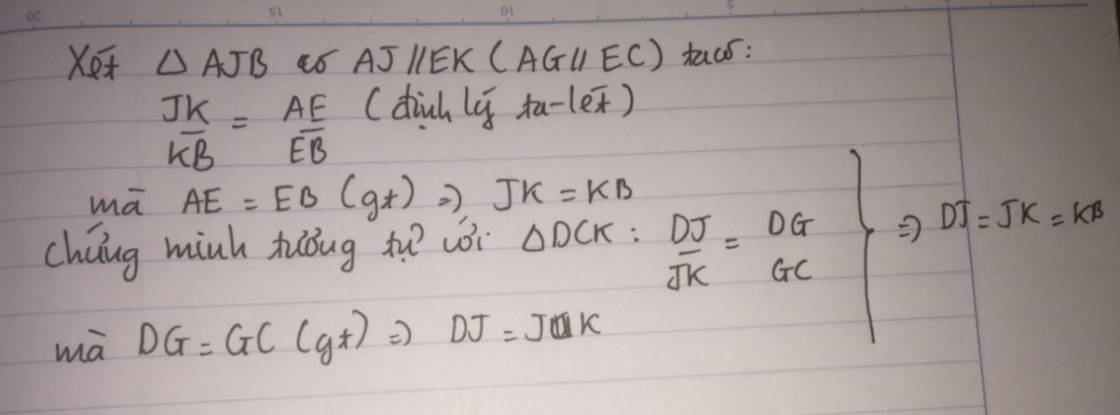
b) Gọi giao điểm của BD với AG ; AF là J;H
DG//AB ; AG ∩ DB = J
Áp dụng định lí Talet ta có :
\(\frac{DG}{AB}=\frac{DJ}{JB}=\frac{1}{2}\Rightarrow DJ=\frac{1}{2}.JB\)
=> DJ = \(\frac{1}{3}.DB\)
amtt HB = \(\frac{1}{3}.DB\)
Mà DJ + JH + HB = DB
=> JH = 1/3 . BD
=> DJ = JH= HB
=> AG; AF chia BD thành 2 đoạn bằng nhau => đpcm