

a...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
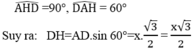
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
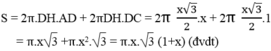
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
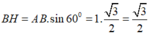
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
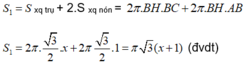

Hướng dẫn làm bài:
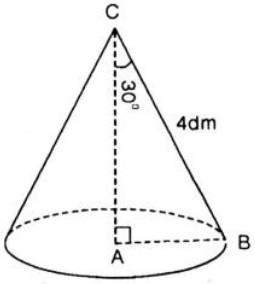
Trong tam giác vuông ABC, ta có:
AB=BC.sinC=BC.sin300=4.1/2=2(dm)
AC=BC.cosC=BC.cos300=4.√3/2=2√3(dm)
Ta có: Sxq = πRl = π. 2. 4 = 8 π (dm2)
V=1/3 π R2 h=1/3 π.22.2√3=8√3.π/3(dm3)

Theo đề bài ta có:
Diện tích hình chữ nhật ABCD là: AB.AD=2a\(^2\) (1)
Chu vi hình chữ nhật là: 2(AB+CD)=6a⇒AB+CD=3a ( 2 )
Từ (1) và (2), ta có ABAB và CDCD là nghiệm của phương trình:
x\(^2\)− 3ax − 2a\(^2\)=0
Giải phương trình ta được: x\(_1\)= 2a; x\(_2\)=a
Theo giả thiết AB>AD nên ta chọn AB=2a; AD=a
Khi quay hình chữ nhật quanh ABAB ta được hình trụ có h=AB=2a và r=AD=a
Vậy diện tích xung quanh hình trụ là:
Sxq=2π.AD.AB=2π.a.2a=4πa\(^2\)
Thể tích hình trụ là:
V=π.AD2.AB=π.a\(^2\).2a=2πa\(^3\)

A D M N P Q B C
Giải:
Ta có: \(\widehat{DAB}=120^0\left(gt\right)\) nên \(\widehat{ADC}=60^0\)
Đường phân giác của \(\widehat{A}\) cắt đường phân giác của \(\widehat{D}\) tại \(M\) thì \(\Delta ADM\) có hai góc bằng \(60^0\) và \(30^0\) nên các đường phân giác đó vuông góc với nhau.
Lập luận tương tự chứng tỏ tứ giác \(MNPQ\) có \(4\) góc vuông nên nó là hình chữ nhật.
Trong tam giác vuông \(ADM\) có:
\(DM=AD\sin\widehat{DAM}=b\sin60^0=\dfrac{b\sqrt{3}}{2}\)
Trong tam giác vuông \(DCN\) và có:
\(DN=DC\sin\widehat{DCN}=a\sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow MN=DN-DM=\left(a-b\right)\dfrac{\sqrt{3}}{2}\)
Trong tam giác vuông \(DCN\) có \(CN=CD\cos60^0=\dfrac{a}{2}\)
Trong tam giác vuông \(BCP\) có \(CP=CB\cos60^0=\dfrac{b}{2}\)
Vậy \(NP=CN-CP=\dfrac{a-b}{2}\)
Suy ra diện tích hình chữ nhật \(MNPQ\) là:
\(MN.NP=\left(a-b\right)^2\dfrac{\sqrt{3}}{4}\left(đvdt\right)\)

.png)
a) Xét hình bình hành ABCD có I, K là trung điểm của AB và DC nên IK là đường trung bình. Vậy thì IK = BC = AD.
Xét tứ giác ADKI có 4 cạnh bằng nhau nên nó là hình thoi.
b) Chứng minh tương tự, ta có KCBI là hình thoi.
Vậy thì KA là phân giác góc \(\widehat{DKI}\) , KB là phân giác góc \(\widehat{IKC}\)
Vậy nên \(\widehat{AKB}=\widehat{AKI}+\widehat{IKB}=\frac{1}{2}\widehat{DKI}+\frac{1}{2}\widehat{IKC}=\frac{1}{2}.180^o=90^o\)
Vậy \(\widehat{AKB}=90^o\)
c) Do AB = DC = 2 BC = 2AD nên chu vi hình bình hành bằng 6 lần BC. Vậy BC = 30 : 6 = 5 (cm)
AB = 2 x 5 = 10 (cm)
Do IKCB là hình thoi nên BK là phân giác góc IBC. Vậy nên \(\widehat{IBK}=60^o\)
Suy ra IBK là tam giác đều hay KB = IK = BC = 5(cm)
Áp dụng định lý Pi-ta-go, ta có: \(AK=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
Vậy diện tích tam giác AKB bằng: \(\frac{1}{2}.5.5\sqrt{3}=\frac{25}{2}\sqrt{3}\left(cm^2\right)\)
Dễ thấy diện tích hình bình hành gấp đôi diện tích tam giác AKB nên \(S_{ABCD}=25\sqrt{3}\left(cm^2\right)\)