Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
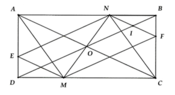
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.
Sửa đề: Cho hình thang ABCD có AB//CD
a: Xét ΔADC có OM//DC
nên \(\frac{AM}{AD}=\frac{AO}{AC}\left(1\right)\)
Xét ΔBAC có ON//AB
nên \(\frac{OC}{OA}=\frac{CN}{NB}\)
=>\(\frac{AO}{OC}=\frac{BN}{NC}\)
=>\(\frac{AO}{OC+OA}=\frac{BN}{BN+NC}\)
=>\(\frac{AO}{AC}=\frac{BN}{BC}\left(2\right)\)
Từ (1),(2) suy ra \(\frac{AM}{AD}=\frac{BN}{BC}\)
b: Xét tứ giác DMOE có
MO//DE
OE//MD
Do đó: DMOE là hình bình hành
=>DM=OE; DE=OM
Xét ΔADC có MO//DC
nên \(\frac{MO}{DC}=\frac{AM}{AD}\)
c: Xét ΔBDC có ON//DC
nên \(\frac{ON}{DC}=\frac{BN}{BC}\)
mà \(\frac{MO}{DC}=\frac{AM}{AD}\)
và \(\frac{BN}{BC}=\frac{AM}{AD}\)
nên OM=ON(1)
Xét tứ giác FCNO có
FC//NO
FO//NC
Do đó: FCNO là hình bình hành
=>FC=ON(2)
Từ (1),(2) suy ra FC=OM
mà OM=DE
nên FC=DE
d: Xét ΔDAB có OM//AB
nên \(\frac{OM}{AB}=\frac{DM}{DA}\)
Xét ΔADC có OM//DC
nên \(\frac{OM}{DC}=\frac{AM}{AD}\)
\(\frac{OM}{AB}+\frac{OM}{DC}=\frac{DM}{DA}+\frac{AM}{AD}=1\)
=>\(OM\left(\frac{1}{AB}+\frac{1}{DC}\right)=1\)
=>\(\frac{1}{AB}+\frac{1}{DC}=\frac{1}{OM}=\frac{2}{MN}\)