Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
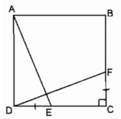
Xét ∆ ADE và ∆ DCF:
AD = DC (gt)
∠ A = ∠ D = 90 °
DE = CF (gt)
Do đó: ∆ ADE = ∆ DCF (c.g.c)
⇒ AE = DF
∠ (EAD) = ∠ (FDC)
∠ (EAD) + ∠ (DEA) = 90 ° (vì ΔADE vuông tại A)
⇒ ∠ (FDC) + ∠ (DEA) = 90 °
Gọi I là giao điểm của AE và DF.
Suy ra: ∠ (IDE) + ∠ (DEI) = 90 °
Trong ∆ DEI ta có: ∠ (DIE) = 180 ° – ( ∠ (IDE) + ∠ (DEI) ) = 180 ° – 90 ° = 90 °
Suy ra: AE ⊥ DF
1) Vì ABCD là hình bình hành nên AB//CD hay AE//CF
Xét tứ giác AECF có AE//CF, AE=CF
=> AECF là hình bình hành
2) Vì AbCDlà hình bình hành nên O là trung điểm của AC (1)
Mà AECF là hình bình hành có 2 đường chéo AC và EF cắt nhau tại O (2)
Suy ra O là trung điểm của EF
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét tứ giác AECF:
AB // CD (gt)
⇒ AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ AC và EF cắt nhau tại trung điểm mỗi đường
OA = OC ( tính chất hình bình hành) ⇒ EF đi qua O
Vậy AC, BD, EF đồng quy tại O.
Hình bình hành ABCD có :
AC cắt BD tại trung điểm của AC và BD ( 1 )
Hình bình hành EBFD có :
EF cắt BD tại trung điểm của EF và BD ( 2 )
\(\Rightarrow\)Từ ( 1 ) và ( 2 ) suy ra AC ; BD ; EF đồng quy
