Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
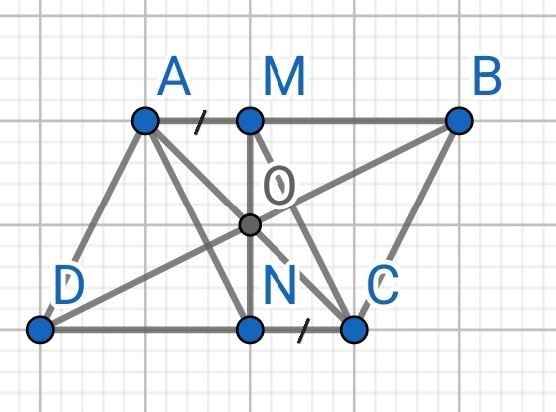a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN
Hình bình hành ABCD . Trên cạnh AB và CD lấy M và N sao cho AM và CN .
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
a: Ta có: AM+MB=AB
CP+PD=CD
AQ+QD=AD
CN+NB=CB
mà AM=CP=AQ=CN và AB=CD=AD=CB
nên MB=PD=QD=NB
Xét tứ giác BMDP có
BM//DP
BM=DP
Do đó: BMDP là hình bình hành
b: ABCD là hình thoi
=>AC⊥BD tại O và O là trung điểm chung của AC và BD
Xét tứ giác BNDQ có
BN//DQ
BN=DQ
Do đó: BNDQ là hình bình hành
=>BD cắt NQ tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của NQ
=>N,O,Q thẳng hàng
c: AMCP là hình bình hành
=>AC cắt MP tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MP
ΔAMQ cân tại A
=>\(\hat{AMQ}=\frac{180^0-\hat{MAQ}}{2}=\frac{180^0-\hat{BAD}}{2}\left(1\right)\)
ΔABD cân tại A
=>\(\hat{ABD}=\frac{180^0-\hat{BAD}}{2}\left(2\right)\)
Từ (1),(2) suy ra \(\hat{AMQ}=\hat{ABD}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên MQ//BD
Ta có: DQ=DP
=>ΔDQP cân tại D
=>\(\hat{DQP}=\frac{180^0-\hat{QDP}}{2}=\frac{180^0-\hat{ADC}}{2}\left(3\right)\)
ΔDAC cân tại D
=>\(\hat{DAC}=\frac{180^0-\hat{ADC}}{2}\left(4\right)\)
Từ (3),(4) suy ra \(\hat{DQP}=\hat{DAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên PQ//AC
mà AC⊥BD
nên PQ⊥BD
Ta có: PQ⊥BD
QM//BD
DO đó: QM⊥QP
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
=>MNPQ là hình bình hành
Hình bình hành MNPQ có QM⊥QP
nên MNPQ là hình chữ nhật
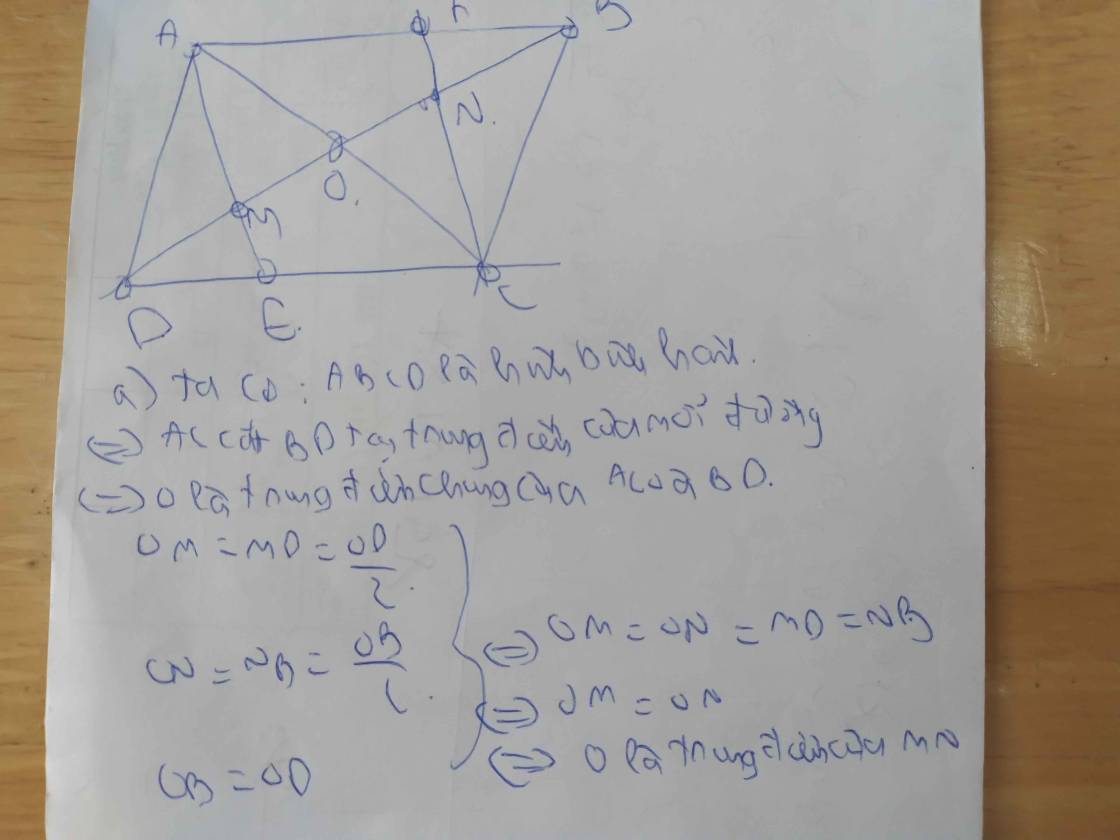
Ta có : AB//CD ( ABCD là HBH )
=> AM//CN và AM=CN (gt)
=> AMCN là HBH
Ta lại có : AC cắt BD tại O
Hay O là trung điểm của AC và DB
Mà : AMCN là HBH
=> O cũng là trung điểm của MN và M,O,N thẳng hàng .